Breaking Fermat (Part 3 of 3)
How did Wiles prove FLT? I love that story, and there is a great book that recounts all that. Fermat claimed that he had a beautiful proof but never wrote it down. Most experts in the field today believe that he thought he had a proof, but it was probably incomplete, or maybe they are just underestimating Fermat's math ability.
Before we get to Wiles', there is one guy who will play a major role in the final proof: Galois. This French mathematician came up with something called "Galois Representation" which will play a crucial role. Sadly Galois was having an affair with a hot woman who was married to the best sword duelist in town, and in a fateful duel Galois was killed, still very young.
In the centuries that came after Fermat stated his conjecture, the proofs were going nowhere. People were proving it for "N=3". Then "N=7 and N=11". Then for "N of the form 2K+77" or things of that nature. Of course at this pace a final proof would never take place.
The first real step towards the proof came in the mid 1950's when Taniyama and Shimura (TaS) proposed a weird conjecture: "Every elliptic curve is a modular form".
Elliptic curves are curves in the following structure: y^2 = ax^3 + bx^2 +cx + d. If you plot this curve on a chart you will see weird, not very symmetric forms. For example, plotting the curve y^2 = x^3 - 2x shows this beautiful shape:
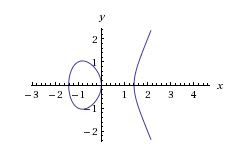
Modular forms are exquisite mathematical objects that obey a massive number of symmetric rules, which have nothing to do with elliptic curves. The conjecture suggests that these two structures are essentially the same: that given an elliptic curve one can always generate a unique modular form, and similarly given a modular form one can always generate a unique elliptic curve. The weirdness of this conjecture is immense: it is correlating completely different mathematical structures. No one had any idea whether this was really true and moreover, no idea on how to even think about how to approach a potential proof to it. To some degree, this was harder than FLT. But so far it has absolutely nothing to do with FLT.
Time goes by and in the mid 1980's a mathematician named Ken Ribet comes up with something that would finally tie TaS with FLT: he assumed that FLT was false, that is, that there existed an A, B and C (positive integers) such that A^n + B^n = C^n, for some n>2. With that assumption, he came up with a weird, never seen before, elliptic curve: y^2 = x(x-A^n)(x+B^n). The interesting aspect of this elliptic curve is that it is proved not to be modular. But remember that TaS claims that every elliptic curve is modular. All Wiles had to do now was to prove TaS. If TaS was proved, by contradiction the funny elliptic curve y^2 = x(x-A^n)(x+B^n) where A^n + B^n = C^n could not exist, hence FLT would have to be true. That was all Wiles had to prove: that TaS was true. Easier said than done....
No one knew how to approach TaS.
Wiles first insight was the following: there are two types of elliptic curves: the semi-stable ones and the un-stable ones. The former ones are tough. The latter ones, tougher. Luckily for Wiles, y^2 = x(x-A^n)(x+B^n) was a semi-stable elliptic curve. Hence he decided not to prove TaS for ALL elliptic curves, but rather only for the semi-stable ones. Slightly less impossible.
The second insight by Wiles was to use Galois Representation. The way that he will try to prove that TaS (for semi-stable elliptic curves) is true was by using set theory: he first would like to represent all semi-stable elliptic curves as an infinite set of all possible semi-stable elliptic curves (EC):
EC = {curve1, curve2, curve3, ...., curveN, ...}
Similarly he would like to represent all modular forms (MF) as an infinite set:
MF = {form1, form2, form3, ..., formN, ...}
And finally he would like to prove that:
a) Given any curve in EC, it always uniquely maps to a form in MF, AND
b) Given any form in MF, it always uniquely maps to a curve in EC
The problem is that these are very different beasts. In order to bring some commonality, he uses Galois Representation to transform these sets into a common language. From that point on, I have no idea what he does but he proves that the two sets are identical. An analogy would be to prove that the set of non-negative natural numbers (NN) is the same as the set of non-negative even numbers (EN), that is:
NN = {0,1,2,3,....}
EN = {0,2,4,6,.....}
And the way to prove is this:
a) Given a number x in NN, this number uniquely maps to number 2x in EN.
b) Given a number y in EN, this number uniquely maps to number y/2 in NN.
That means that NN and EN are essentially the same: given one set, you can always generate the other one in a unique way.
Wiles did the same for EC and MF. Since both sets are a proper match, he then proved that "Any semi-stable elliptic curve is a modular form". But if FLT is false, it implies a semi-stable elliptic curve without a modular form. Therefore, FLT is true. End of proof. If Fermat was alive, he would just have said: "See, I told you so!!!"
Marcelo
Before we get to Wiles', there is one guy who will play a major role in the final proof: Galois. This French mathematician came up with something called "Galois Representation" which will play a crucial role. Sadly Galois was having an affair with a hot woman who was married to the best sword duelist in town, and in a fateful duel Galois was killed, still very young.
In the centuries that came after Fermat stated his conjecture, the proofs were going nowhere. People were proving it for "N=3". Then "N=7 and N=11". Then for "N of the form 2K+77" or things of that nature. Of course at this pace a final proof would never take place.
The first real step towards the proof came in the mid 1950's when Taniyama and Shimura (TaS) proposed a weird conjecture: "Every elliptic curve is a modular form".
Elliptic curves are curves in the following structure: y^2 = ax^3 + bx^2 +cx + d. If you plot this curve on a chart you will see weird, not very symmetric forms. For example, plotting the curve y^2 = x^3 - 2x shows this beautiful shape:

Time goes by and in the mid 1980's a mathematician named Ken Ribet comes up with something that would finally tie TaS with FLT: he assumed that FLT was false, that is, that there existed an A, B and C (positive integers) such that A^n + B^n = C^n, for some n>2. With that assumption, he came up with a weird, never seen before, elliptic curve: y^2 = x(x-A^n)(x+B^n). The interesting aspect of this elliptic curve is that it is proved not to be modular. But remember that TaS claims that every elliptic curve is modular. All Wiles had to do now was to prove TaS. If TaS was proved, by contradiction the funny elliptic curve y^2 = x(x-A^n)(x+B^n) where A^n + B^n = C^n could not exist, hence FLT would have to be true. That was all Wiles had to prove: that TaS was true. Easier said than done....
No one knew how to approach TaS.
Wiles first insight was the following: there are two types of elliptic curves: the semi-stable ones and the un-stable ones. The former ones are tough. The latter ones, tougher. Luckily for Wiles, y^2 = x(x-A^n)(x+B^n) was a semi-stable elliptic curve. Hence he decided not to prove TaS for ALL elliptic curves, but rather only for the semi-stable ones. Slightly less impossible.
The second insight by Wiles was to use Galois Representation. The way that he will try to prove that TaS (for semi-stable elliptic curves) is true was by using set theory: he first would like to represent all semi-stable elliptic curves as an infinite set of all possible semi-stable elliptic curves (EC):
EC = {curve1, curve2, curve3, ...., curveN, ...}
Similarly he would like to represent all modular forms (MF) as an infinite set:
MF = {form1, form2, form3, ..., formN, ...}
And finally he would like to prove that:
a) Given any curve in EC, it always uniquely maps to a form in MF, AND
b) Given any form in MF, it always uniquely maps to a curve in EC
The problem is that these are very different beasts. In order to bring some commonality, he uses Galois Representation to transform these sets into a common language. From that point on, I have no idea what he does but he proves that the two sets are identical. An analogy would be to prove that the set of non-negative natural numbers (NN) is the same as the set of non-negative even numbers (EN), that is:
NN = {0,1,2,3,....}
EN = {0,2,4,6,.....}
And the way to prove is this:
a) Given a number x in NN, this number uniquely maps to number 2x in EN.
b) Given a number y in EN, this number uniquely maps to number y/2 in NN.
That means that NN and EN are essentially the same: given one set, you can always generate the other one in a unique way.
Wiles did the same for EC and MF. Since both sets are a proper match, he then proved that "Any semi-stable elliptic curve is a modular form". But if FLT is false, it implies a semi-stable elliptic curve without a modular form. Therefore, FLT is true. End of proof. If Fermat was alive, he would just have said: "See, I told you so!!!"
Marcelo


What a story Marcelo - it even has love, passion and death involved thanks to a note about Galois! Also, you managed to not use a word "isomorphism" :) Looking forward to new stories!
ReplyDeleteThanks buddy, indeed the right term would have been isomorphism :) the story is much more intricate and funny than just what I described. Have a wonderful day today!!!!
ReplyDelete