LeetCode Hard Problem
Problem is here: https://leetcode.com/problems/closest-binary-search-tree-value-ii/
I managed to solve this problem in NLogN. Initially I thought this would not work since the problem is suggesting a less-than O(n) solution, but I gave it a try anyways.
To solve in NLogN one approach is the following:
The most expensive step is #3, which costs NLogN. Notice that we also use O(N)-space, which isn't ideal.
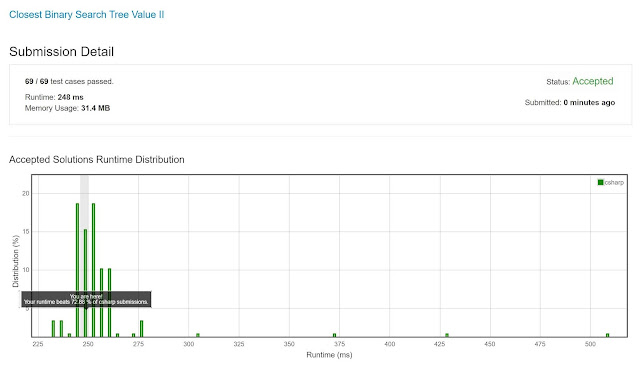
When I put it to the test, the result was better than I expected. Code is below, cheers, ACC.
public class Solution
{
public IList<int> ClosestKValues(TreeNode root, double target, int k)
{
PriorityQueue pQueue = new PriorityQueue();
PopulatePQueue(root, target, pQueue);
List<int> retVal = new List<int>();
for (int i = 0; i < k; i++)
{
retVal.Add((int)pQueue.Dequeue());
}
return retVal;
}
private void PopulatePQueue(TreeNode node, double target, PriorityQueue pQueue)
{
if (node == null) return;
pQueue.Enqueue(node.val, Math.Abs(node.val - target));
PopulatePQueue(node.left, target, pQueue);
PopulatePQueue(node.right, target, pQueue);
}
}
public class PriorityQueue
{
public struct HeapEntry
{
private object item;
private double priority;
public HeapEntry(object item, double priority)
{
this.item = item;
this.priority = priority;
}
public object Item
{
get
{
return item;
}
}
public double Priority
{
get
{
return priority;
}
}
}
private int count;
private int capacity;
private HeapEntry[] heap;
public int Count
{
get
{
return this.count;
}
}
public PriorityQueue()
{
capacity = 100000;
heap = new HeapEntry[capacity];
}
public object Dequeue(/*ref long weight*/)
{
object result = heap[0].Item;
//weight = heap[0].Priority;
count--;
trickleDown(0, heap[count]);
return result;
}
public void Enqueue(object item, double priority)
{
count++;
bubbleUp(count - 1, new HeapEntry(item, priority));
}
private void bubbleUp(int index, HeapEntry he)
{
int parent = (index - 1) / 2;
// note: (index > 0) means there is a parent
while ((index > 0) && (heap[parent].Priority > he.Priority))
{
heap[index] = heap[parent];
index = parent;
parent = (index - 1) / 2;
}
heap[index] = he;
}
private void trickleDown(int index, HeapEntry he)
{
int child = (index * 2) + 1;
while (child < count)
{
if (((child + 1) < count) &&
(heap[child].Priority > heap[child + 1].Priority))
{
child++;
}
heap[index] = heap[child];
index = child;
child = (index * 2) + 1;
}
bubbleUp(index, he);
}
}
272. Closest Binary Search Tree Value II
Hard
Given a non-empty binary search tree and a target value, find k values in the BST that are closest to the target.
Note:
- Given target value is a floating point.
- You may assume k is always valid, that is: k ≤ total nodes.
- You are guaranteed to have only one unique set of k values in the BST that are closest to the target.
Example:
Input: root = [4,2,5,1,3], target = 3.714286, and k = 2 4 / \ 2 5 / \ 1 3 Output: [4,3]
Follow up:
Assume that the BST is balanced, could you solve it in less than O(n) runtime (where n = total nodes)?
Assume that the BST is balanced, could you solve it in less than O(n) runtime (where n = total nodes)?
Accepted
50,428
Submissions
103,444
I managed to solve this problem in NLogN. Initially I thought this would not work since the problem is suggesting a less-than O(n) solution, but I gave it a try anyways.
To solve in NLogN one approach is the following:
- Have a priority queue (I changed my implementation to take a double as priority instead of long - trivial change)
- Unfortunately, ignore the BST properties
- Perform a full pre-order DFS traversal of the tree. Add each element to the priority queue with priority |node.val - target|
- After that, retrieve the top K elements from the priority queue (it can be done in K*LogN time)
The most expensive step is #3, which costs NLogN. Notice that we also use O(N)-space, which isn't ideal.
When I put it to the test, the result was better than I expected. Code is below, cheers, ACC.
public class Solution
{
public IList<int> ClosestKValues(TreeNode root, double target, int k)
{
PriorityQueue pQueue = new PriorityQueue();
PopulatePQueue(root, target, pQueue);
List<int> retVal = new List<int>();
for (int i = 0; i < k; i++)
{
retVal.Add((int)pQueue.Dequeue());
}
return retVal;
}
private void PopulatePQueue(TreeNode node, double target, PriorityQueue pQueue)
{
if (node == null) return;
pQueue.Enqueue(node.val, Math.Abs(node.val - target));
PopulatePQueue(node.left, target, pQueue);
PopulatePQueue(node.right, target, pQueue);
}
}
public class PriorityQueue
{
public struct HeapEntry
{
private object item;
private double priority;
public HeapEntry(object item, double priority)
{
this.item = item;
this.priority = priority;
}
public object Item
{
get
{
return item;
}
}
public double Priority
{
get
{
return priority;
}
}
}
private int count;
private int capacity;
private HeapEntry[] heap;
public int Count
{
get
{
return this.count;
}
}
public PriorityQueue()
{
capacity = 100000;
heap = new HeapEntry[capacity];
}
public object Dequeue(/*ref long weight*/)
{
object result = heap[0].Item;
//weight = heap[0].Priority;
count--;
trickleDown(0, heap[count]);
return result;
}
public void Enqueue(object item, double priority)
{
count++;
bubbleUp(count - 1, new HeapEntry(item, priority));
}
private void bubbleUp(int index, HeapEntry he)
{
int parent = (index - 1) / 2;
// note: (index > 0) means there is a parent
while ((index > 0) && (heap[parent].Priority > he.Priority))
{
heap[index] = heap[parent];
index = parent;
parent = (index - 1) / 2;
}
heap[index] = he;
}
private void trickleDown(int index, HeapEntry he)
{
int child = (index * 2) + 1;
while (child < count)
{
if (((child + 1) < count) &&
(heap[child].Priority > heap[child + 1].Priority))
{
child++;
}
heap[index] = heap[child];
index = child;
child = (index * 2) + 1;
}
bubbleUp(index, he);
}
}


Comments
Post a Comment