A brute-force approach for Max BST

I've tried this problem before, twice, with no luck. I remember trying an O(N)-time solution, but got wrong answers twice. Decided to go for an N^2 solution, this time it worked. Here is the problem: Largest BST Subtree - LeetCode

333. Largest BST Subtree

Medium

Given the root of a binary tree, find the largest subtree, which is also a Binary Search Tree (BST), where the largest means subtree has the largest number of nodes.

A Binary Search Tree (BST) is a tree in which all the nodes follow the below-mentioned properties:

• The left subtree values are less than the value of their parent (root) node's value.
• The right subtree values are greater than the value of their parent (root) node's value.

Note: A subtree must include all of its descendants.

Follow up: Can you figure out ways to solve it with O(n) time complexity?

 

Example 1:

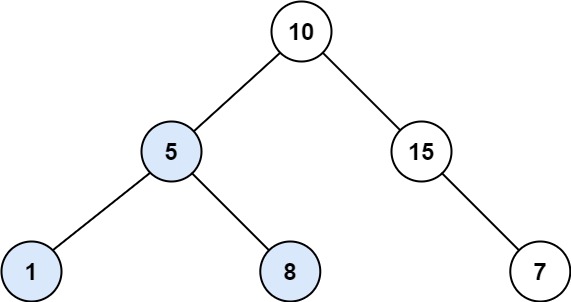
Input: root = [10,5,15,1,8,null,7]
Output: 3
Explanation: The Largest BST Subtree in this case is the highlighted one. The return value is the subtree's size, which is 3.

Example 2:

Input: root = [4,2,7,2,3,5,null,2,null,null,null,null,null,1]
Output: 2

 

Constraints:

• The number of nodes in the tree is in the range [0, 104].
• -104 <= Node.val <= 104

Accepted

59,902

Submissions

157,343

The approach that I took was an N^2 one:

1/ Create a method that checks whether a given node is the root of a BST. Do it using post-order (in-order only really works if the tree contains only unique elements). This is an O(N)

2/ As part of (1), make it return the number of nodes in the subtree (no extra time added)

3/ Finally call it for each subnode in the tree. Another O(N)

Combined this would be O(N^2). Since N=10000, we're talking about 10^8. I thought it was going to time out - it didn't. Code is below, cheers, ACC.

public int LargestBSTSubtree(TreeNode root)
{
    int retVal = 0;
    LargestBSTSubtree(root, ref retVal);
    return retVal;
}

private void LargestBSTSubtree(TreeNode node, ref int maxNodes)
{
    if (node == null) return;

    int max = Int32.MinValue;
    int min = Int32.MaxValue;
    int numberNodes = 0;

    if (IsBST(node, ref max, ref min, ref numberNodes))
    {
        maxNodes = Math.Max(maxNodes, numberNodes);
    }

    LargestBSTSubtree(node.left, ref maxNodes);
    LargestBSTSubtree(node.right, ref maxNodes);
}

private bool IsBST(TreeNode node, ref int max, ref int min, ref int numberNodes)
{
    if (node == null) return true;

    int leftMax = Int32.MinValue;
    int leftMin = Int32.MaxValue;
    int leftNumberNodes = 0;
    if (!IsBST(node.left, ref leftMax, ref leftMin, ref leftNumberNodes)) return false;

    int rightMax = Int32.MinValue;
    int rightMin = Int32.MaxValue;
    int rightNumberNodes = 0;
    if (!IsBST(node.right, ref rightMax, ref rightMin, ref rightNumberNodes)) return false;

    if (leftMax >= node.val) return false;
    if (rightMin <= node.val) return false;

    max = node.val;
    max = Math.Max(max, leftMax);
    max = Math.Max(max, rightMax);

    min = node.val;
    min = Math.Min(min, leftMin);
    min = Math.Min(min, rightMin);

    numberNodes = 1 + leftNumberNodes + rightNumberNodes;

    return true;
}