The Circle Equation

Problem is actually very simple - all you have to do is remember the equality (or inequality) for the circle in 2D. Here it is: Queries on Number of Points Inside a Circle - LeetCode

1828. Queries on Number of Points Inside a Circle

Medium

You are given an array points where points[i] = [xi, yi] is the coordinates of the ith point on a 2D plane. Multiple points can have the same coordinates.

You are also given an array queries where queries[j] = [xj, yj, rj] describes a circle centered at (xj, yj) with a radius of rj.

For each query queries[j], compute the number of points inside the jth circle. Points on the border of the circle are considered inside.

Return an array answer, where answer[j] is the answer to the jth query.

 

Example 1:

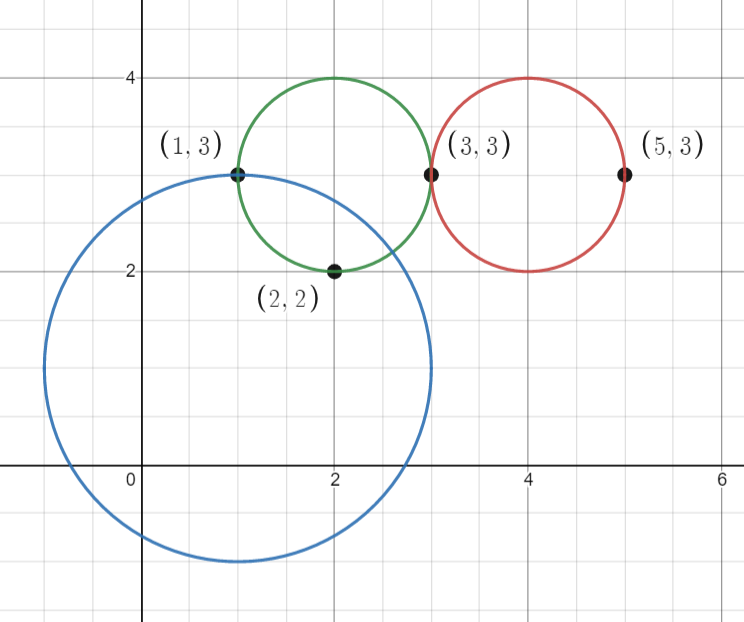
Input: points = [[1,3],[3,3],[5,3],[2,2]], queries = [[2,3,1],[4,3,1],[1,1,2]]
Output: [3,2,2]
Explanation: The points and circles are shown above.
queries[0] is the green circle, queries[1] is the red circle, and queries[2] is the blue circle.

Example 2:

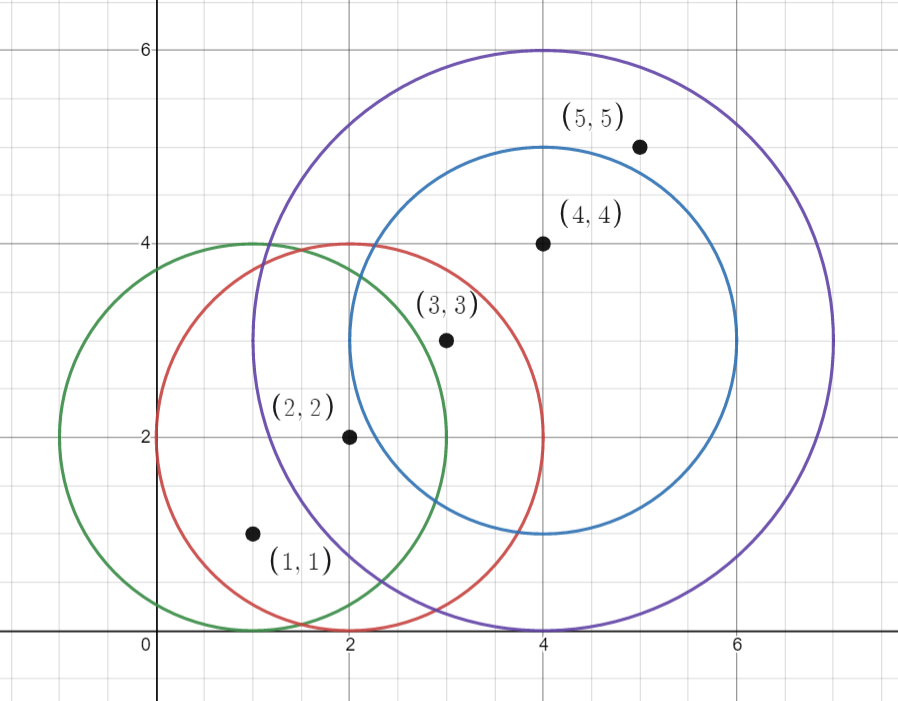
Input: points = [[1,1],[2,2],[3,3],[4,4],[5,5]], queries = [[1,2,2],[2,2,2],[4,3,2],[4,3,3]]
Output: [2,3,2,4]
Explanation: The points and circles are shown above.
queries[0] is green, queries[1] is red, queries[2] is blue, and queries[3] is purple.

 

Constraints:

• 1 <= points.length <= 500
• points[i].length == 2
• 0 <= x​​​​​​i, y​​​​​​i <= 500
• 1 <= queries.length <= 500
• queries[j].length == 3
• 0 <= xj, yj <= 500
• 1 <= rj <= 500
• All coordinates are integers.

 

Follow up: Could you find the answer for each query in better complexity than O(n)?

Accepted

4,435

Submissions

5,077

The solution is O(n*m) but with the small n and m it works fine. The equation for the circle is simple: (x-cx)^2 + (y-cy)^2 = r^2. Since we want the points inside the circle, change the equality with inequality <= r^2. That's it (except that I also transformed the computation to a long to avoid overflow errors). Code is below, cheers!!! ACC

public int[] CountPoints(int[][] points, int[][] queries)
{
    int[] retVal = new int[queries.Length];

    for (int i = 0; i < queries.Length; i++)
    {
        int count = 0;
        for (int j = 0; j < points.Length; j++)
        {
            if (IsPointInsideCircle(points[j][0], points[j][1], queries[i][0], queries[i][1], queries[i][2])) count++;
        }
        retVal[i] = count;
    }

    return retVal;
}

private bool IsPointInsideCircle(int px, int py, int x0, int y0, int r)
{
    return 1L * (px - x0) * (px - x0) + (py - y0) * (py - y0) <= 1L * r * r;
}