Maximal Square: using DP as a helper for an N^3 solution

Problem is to find the max square in a matrix, take a look: Maximal Square - LeetCode

221. Maximal Square

Medium

Given an m x n binary matrix filled with 0's and 1's, find the largest square containing only 1's and return its area.

 

Example 1:

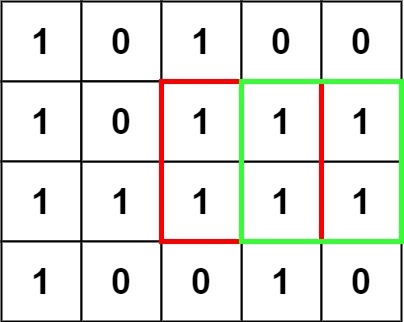
Input: matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
Output: 4

Example 2:

Input: matrix = [["0","1"],["1","0"]]
Output: 1

Example 3:

Input: matrix = [["0"]]
Output: 0

 

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 300
• matrix[i][j] is '0' or '1'.

Accepted

468,284

Submissions

1,087,879

The idea is to use DP as a helper function. Imagine having every cell with two counters: the number of consecutive vertical 1s, and the number of consecutive horizontal 1s. This can be accomplished with DP in O(N^2)-time. Next, we go thru all cells and for each one that has a 1, we walk down the diagonal using the DP values to calculate the maximum square starting at that cell, and we keep track of the overall max. That takes O(N^3)-time. Given N=300, we're talking about 27M interactions which isn't that bad. Code is down below, cheers, ACC.

public class DPSquare
{
    public int verticals = 0;
    public int horizontals = 0;

    public DPSquare(int verticals, int horizontals)
    {
        this.verticals = verticals;
        this.horizontals = horizontals;
    }
}
public int MaximalSquare(char[][] matrix)
{
    DPSquare[][] dp = new DPSquare[matrix.Length][];
    for (int i = 0; i < dp.Length; i++) dp[i] = new DPSquare[matrix[0].Length];

    //DP O(n^2)
    for (int r = 0; r < matrix.Length; r++)
    {
        for (int c = 0; c < matrix[r].Length; c++)
        {
            if (matrix[r][c] == '0')
            {
                dp[r][c] = new DPSquare(0, 0);
            }
            else
            {
                dp[r][c] = new DPSquare(1, 1);
                if (r - 1 >= 0) dp[r][c].verticals += dp[r - 1][c].verticals;
                if (c - 1 >= 0) dp[r][c].horizontals += dp[r][c - 1].horizontals;
            }
        }
    }

    //Calculate max O(n^3)
    int max = 0;
    for (int r = 0; r < matrix.Length; r++)
    {
        for (int c = 0; c < matrix[r].Length; c++)
        {
            if (matrix[r][c] == '1')
            {
                int tempRow = r;
                int tempCol = c;
                while (tempRow < matrix.Length &&
                        tempCol < matrix[r].Length &&
                        matrix[tempRow][tempCol] == '1' &&
                        dp[tempRow][tempCol].verticals >= tempRow - r + 1 &&
                        dp[tempRow][tempCol].horizontals >= tempCol - c + 1)
                {
                    int area = (tempRow - r + 1) * (tempCol - c + 1);
                    max = Math.Max(max, area);
                    tempRow++;
                    tempCol++;
                }
            }
        }
    }

    return max;
}