2^12 is a small number

This problem can certainly be solved with DP, but a simple brute-force approach works. Notice that we have 12 sections, and Bob can choose to win a section, or ignore it. Hence for each one we have 2 options. Or, if we were to try them all, 2^12, which is 4096, which is a tiny number. So I tried it all and it worked. The way to try it all is by doing a tail-end recursion. There is just a small caveat which is that we need to ensure that the number of arrows used by Bob is the same as the number of arrows used by Alice, so you're going to see some calculations here to accomplish that goal. Cheers, ACC.

Maximum Points in an Archery Competition - LeetCode

2212. Maximum Points in an Archery Competition

Medium

Alice and Bob are opponents in an archery competition. The competition has set the following rules:

1. Alice first shoots numArrows arrows and then Bob shoots numArrows arrows.
2. The points are then calculated as follows:
   1. The target has integer scoring sections ranging from 0 to 11 inclusive.
   2. For each section of the target with score k (in between 0 to 11), say Alice and Bob have shot ak and bk arrows on that section respectively. If ak >= bk, then Alice takes k points. If ak < bk, then Bob takes k points.
   3. However, if ak == bk == 0, then nobody takes k points.

• For example, if Alice and Bob both shot 2 arrows on the section with score 11, then Alice takes 11 points. On the other hand, if Alice shot 0 arrows on the section with score 11 and Bob shot 2 arrows on that same section, then Bob takes 11 points.

You are given the integer numArrows and an integer array aliceArrows of size 12, which represents the number of arrows Alice shot on each scoring section from 0 to 11. Now, Bob wants to maximize the total number of points he can obtain.

Return the array bobArrows which represents the number of arrows Bob shot on each scoring section from 0 to 11. The sum of the values in bobArrows should equal numArrows.

If there are multiple ways for Bob to earn the maximum total points, return any one of them.

 

Example 1:

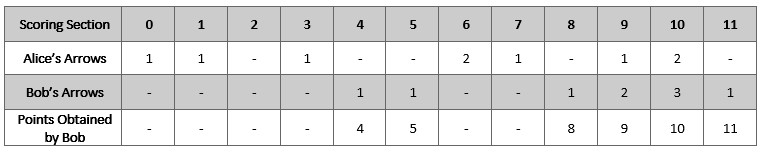
Input: numArrows = 9, aliceArrows = [1,1,0,1,0,0,2,1,0,1,2,0]
Output: [0,0,0,0,1,1,0,0,1,2,3,1]
Explanation: The table above shows how the competition is scored. 
Bob earns a total point of 4 + 5 + 8 + 9 + 10 + 11 = 47.
It can be shown that Bob cannot obtain a score higher than 47 points.

Example 2:

Input: numArrows = 3, aliceArrows = [0,0,1,0,0,0,0,0,0,0,0,2]
Output: [0,0,0,0,0,0,0,0,1,1,1,0]
Explanation: The table above shows how the competition is scored.
Bob earns a total point of 8 + 9 + 10 = 27.
It can be shown that Bob cannot obtain a score higher than 27 points.

 

Constraints:

• 1 <= numArrows <= 105
• aliceArrows.length == bobArrows.length == 12
• 0 <= aliceArrows[i], bobArrows[i] <= numArrows
• sum(aliceArrows[i]) == numArrows

public int[] MaximumBobPoints(int numArrows, int[] aliceArrows)
{
    int[] maxBowArrows = new int[aliceArrows.Length];
    int maxPoints = 0;

    MaximumBobPoints(numArrows,
                        0,
                        aliceArrows,
                        new int[aliceArrows.Length],
                        aliceArrows.Length - 1,
                        0,
                        ref maxPoints,
                        ref maxBowArrows);

    return maxBowArrows;
}

private void MaximumBobPoints(int numArrows,
                                int currentNumArrows,
                                int[] aliceArrows,
                                int[] bobArrows,
                                int index,
                                int currentPoints,
                                ref int maxPoints,
                                ref int[] maxBoxArrows)
{
    if (currentNumArrows > numArrows) return;

    if (index < 0)
    {
        if (currentPoints > maxPoints)
        {
            maxPoints = currentPoints;
            maxBoxArrows = (int[])bobArrows.Clone();

            if (currentNumArrows < numArrows)
            {
                int delta = numArrows - currentNumArrows;
                maxBoxArrows[0] += delta;
            }
        }
        return;
    }

    if (currentNumArrows == numArrows)
    {
        if (currentPoints > maxPoints)
        {
            maxPoints = currentPoints;
            maxBoxArrows = (int[])bobArrows.Clone();
        }
        return;
    }

    //Case 1: use the index
    if (currentNumArrows + aliceArrows[index] + 1 <= numArrows)
    {
        int temp = bobArrows[index];
        bobArrows[index] = aliceArrows[index] + 1;
        MaximumBobPoints(numArrows,
                            currentNumArrows + aliceArrows[index] + 1,
                            aliceArrows,
                            bobArrows,
                            index - 1,
                            currentPoints + index,
                            ref maxPoints,
                            ref maxBoxArrows);
        bobArrows[index] = temp;
    }

    //Case 2: skip
    MaximumBobPoints(numArrows,
                        currentNumArrows,
                        aliceArrows,
                        bobArrows,
                        index - 1,
                        currentPoints,
                        ref maxPoints,
                        ref maxBoxArrows);
}