Saturday Night Dijkstra's Algorithm II
Another problem that requires use of Dijkstra's Algorithm for efficiency's purposes. Basically we have a directed weighted graph, and want to find the min distance between a certain node and any marked node. Approach goes as follows:
1/ Build a quick-access graph using a hashtable. Remember that you can have multiple edges [u,v,w] where u and v are the same. Handle that in the creation method
2/ Make a quick-access look-up table for the marked nodes
3/ Use a ascending priority queue to speed up the BFS algorithm
4/ As you do the BFS, unfortunately there is no easy way to stop it since you may always find a min route. Instead, rely on the pruning to not add to the queue any path larger than the min so far
5/ Handle some edge cases here and there, such as no-path found
Code is down below, cheers, ACC
Find the Closest Marked Node - LeetCode
You are given a positive integer n which is the number of nodes of a 0-indexed directed weighted graph and a 0-indexed 2D array edges where edges[i] = [ui, vi, wi] indicates that there is an edge from node ui to node vi with weight wi.
You are also given a node s and a node array marked; your task is to find the minimum distance from s to any of the nodes in marked.
Return an integer denoting the minimum distance from s to any node in marked or -1 if there are no paths from s to any of the marked nodes.
Example 1:
Input: n = 4, edges = [[0,1,1],[1,2,3],[2,3,2],[0,3,4]], s = 0, marked = [2,3] Output: 4 Explanation: There is one path from node 0 (the green node) to node 2 (a red node), which is 0->1->2, and has a distance of 1 + 3 = 4. There are two paths from node 0 to node 3 (a red node), which are 0->1->2->3 and 0->3, the first one has a distance of 1 + 3 + 2 = 6 and the second one has a distance of 4. The minimum of them is 4.
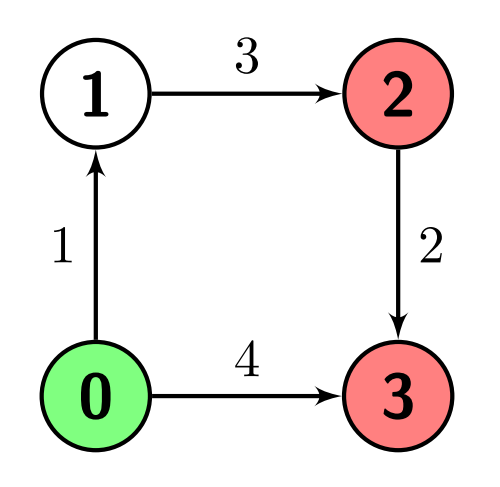
Example 2:
Input: n = 5, edges = [[0,1,2],[0,2,4],[1,3,1],[2,3,3],[3,4,2]], s = 1, marked = [0,4] Output: 3 Explanation: There are no paths from node 1 (the green node) to node 0 (a red node). There is one path from node 1 to node 4 (a red node), which is 1->3->4, and has a distance of 1 + 2 = 3. So the answer is 3.
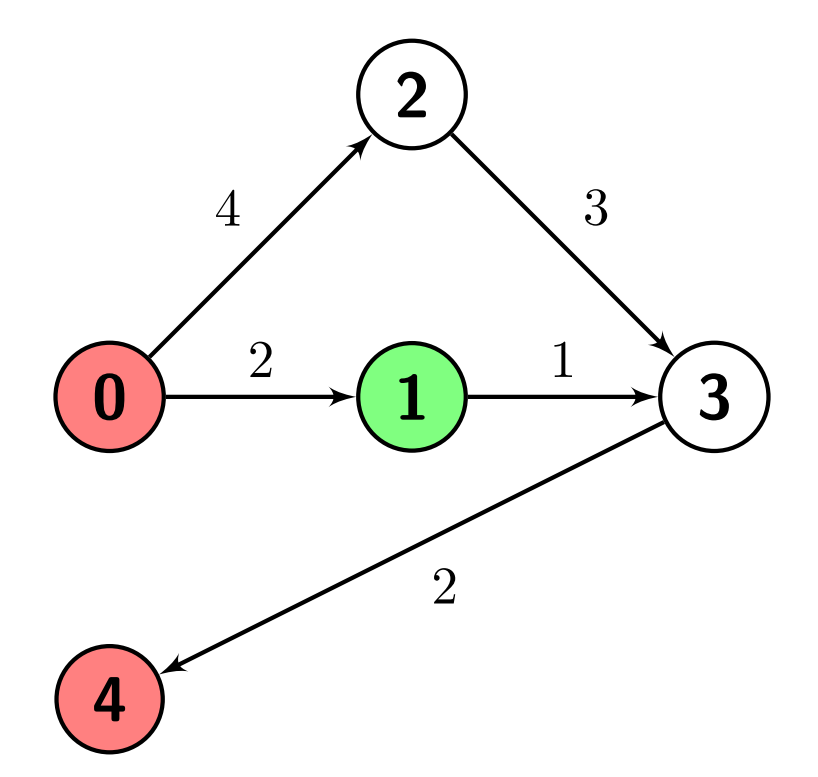
Example 3:
Input: n = 4, edges = [[0,1,1],[1,2,3],[2,3,2]], s = 3, marked = [0,1] Output: -1 Explanation: There are no paths from node 3 (the green node) to any of the marked nodes (the red nodes), so the answer is -1.

Constraints:
2 <= n <= 5001 <= edges.length <= 104edges[i].length = 30 <= edges[i][0], edges[i][1] <= n - 11 <= edges[i][2] <= 1061 <= marked.length <= n - 10 <= s, marked[i] <= n - 1s != marked[i]marked[i] != marked[j]for everyi != j- The graph might have repeated edges.
- The graph is generated such that it has no self-loops.
public class Solution
{
public int MinimumDistance(int n, IList> edges, int s, int[] marked)
{
Hashtable graph = CreateGraphFromEdges(edges);
Hashtable htMarked = new Hashtable();
foreach (int m in marked) htMarked.Add(m, true);
Hashtable minWeightNodes = new Hashtable();
for (int i = 0; i < n; i++)
minWeightNodes.Add(i, Int32.MaxValue);
PriorityQueue pQueue = new PriorityQueue(true);
pQueue.Enqueue(s, 0);
minWeightNodes[s] = 0;
int minDistance = Int32.MaxValue;
bool foundSolution = false;
while (pQueue.Count > 0)
{
double temp = 0;
int currentNode = (int)pQueue.Dequeue(out temp);
int currentWeight = (int)temp;
if (htMarked.ContainsKey(currentNode) && currentWeight < minDistance)
{
foundSolution = true;
minDistance = currentWeight;
}
if (graph.ContainsKey(currentNode))
{
Hashtable connections = (Hashtable)graph[currentNode];
foreach (int node in connections.Keys)
{
if (currentWeight + (int)connections[node] <= minDistance && currentWeight + (int)connections[node] <= (int)minWeightNodes[node])
{
minWeightNodes[node] = currentWeight + (int)connections[node];
pQueue.Enqueue(node, (int)minWeightNodes[node]);
}
}
}
}
return foundSolution ? minDistance : -1;
}
private Hashtable CreateGraphFromEdges(IList> edges)
{
Hashtable graph = new Hashtable();
for (int i = 0; i < edges.Count; i++)
{
int from = edges[i][0];
int to = edges[i][1];
int weight = edges[i][2];
if (!graph.ContainsKey(from)) graph.Add(from, new Hashtable());
Hashtable connections = (Hashtable)graph[from];
if (!connections.ContainsKey(to)) connections.Add(to, weight);
else connections[to] = Math.Min((int)connections[to], weight);
}
return graph;
}
public class PriorityQueue
{
public struct HeapEntry
{
private object item;
private double priority;
public HeapEntry(object item, double priority)
{
this.item = item;
this.priority = priority;
}
public object Item
{
get
{
return item;
}
}
public double Priority
{
get
{
return priority;
}
}
}
private bool ascend;
private int count;
private int capacity;
private HeapEntry[] heap;
public int Count
{
get
{
return this.count;
}
}
public PriorityQueue(bool ascend, int cap = -1)
{
capacity = 10000000;
if (cap > 0) capacity = cap;
heap = new HeapEntry[capacity];
this.ascend = ascend;
}
public object Dequeue(out double priority)
{
priority = heap[0].Priority;
object result = heap[0].Item;
count--;
trickleDown(0, heap[count]);
return result;
}
public object Peak(out double priority)
{
priority = heap[0].Priority;
object result = heap[0].Item;
return result;
}
public object Peak(/*out double priority*/)
{
//priority = heap[0].Priority;
object result = heap[0].Item;
return result;
}
public void Enqueue(object item, double priority)
{
count++;
bubbleUp(count - 1, new HeapEntry(item, priority));
}
private void bubbleUp(int index, HeapEntry he)
{
int parent = (index - 1) / 2;
// note: (index > 0) means there is a parent
if (this.ascend)
{
while ((index > 0) && (heap[parent].Priority > he.Priority))
{
heap[index] = heap[parent];
index = parent;
parent = (index - 1) / 2;
}
heap[index] = he;
}
else
{
while ((index > 0) && (heap[parent].Priority < he.Priority))
{
heap[index] = heap[parent];
index = parent;
parent = (index - 1) / 2;
}
heap[index] = he;
}
}
private void trickleDown(int index, HeapEntry he)
{
int child = (index * 2) + 1;
while (child < count)
{
if (this.ascend)
{
if (((child + 1) < count) &&
(heap[child].Priority > heap[child + 1].Priority))
{
child++;
}
}
else
{
if (((child + 1) < count) &&
(heap[child].Priority < heap[child + 1].Priority))
{
child++;
}
}
heap[index] = heap[child];
index = child;
child = (index * 2) + 1;
}
bubbleUp(index, he);
}
}
}




Comments
Post a Comment