Post-Order Traversal and Sorted Lists

Interesting problem combining post-order traversal and sorted lists:

1/ Perform a post-order traversal
2/ On each step, return a sorted list with the smallest K elements in the subtree
3/ Insertion operation and merge of sorted lists done in a custom way for speed

Time complexity around O(number of nodes * k). Code is down below, cheers, ACC.

Count Nodes That Are Great Enough - LeetCode

2792. Count Nodes That Are Great Enough

Medium

You are given a root to a binary tree and an integer k. A node of this tree is called great enough if the followings hold:

• Its subtree has at least k nodes.
• Its value is greater than the value of at least k nodes in its subtree.

Return the number of nodes in this tree that are great enough.

The node u is in the subtree of the node v, if u == v or v is an ancestor of u.

 

Example 1:

Input: root = [7,6,5,4,3,2,1], k = 2
Output: 3
Explanation: Number the nodes from 1 to 7.
The values in the subtree of node 1: {1,2,3,4,5,6,7}. Since node.val == 7, there are 6 nodes having a smaller value than its value. So it's great enough.
The values in the subtree of node 2: {3,4,6}. Since node.val == 6, there are 2 nodes having a smaller value than its value. So it's great enough.
The values in the subtree of node 3: {1,2,5}. Since node.val == 5, there are 2 nodes having a smaller value than its value. So it's great enough.
It can be shown that other nodes are not great enough.
See the picture below for a better understanding.

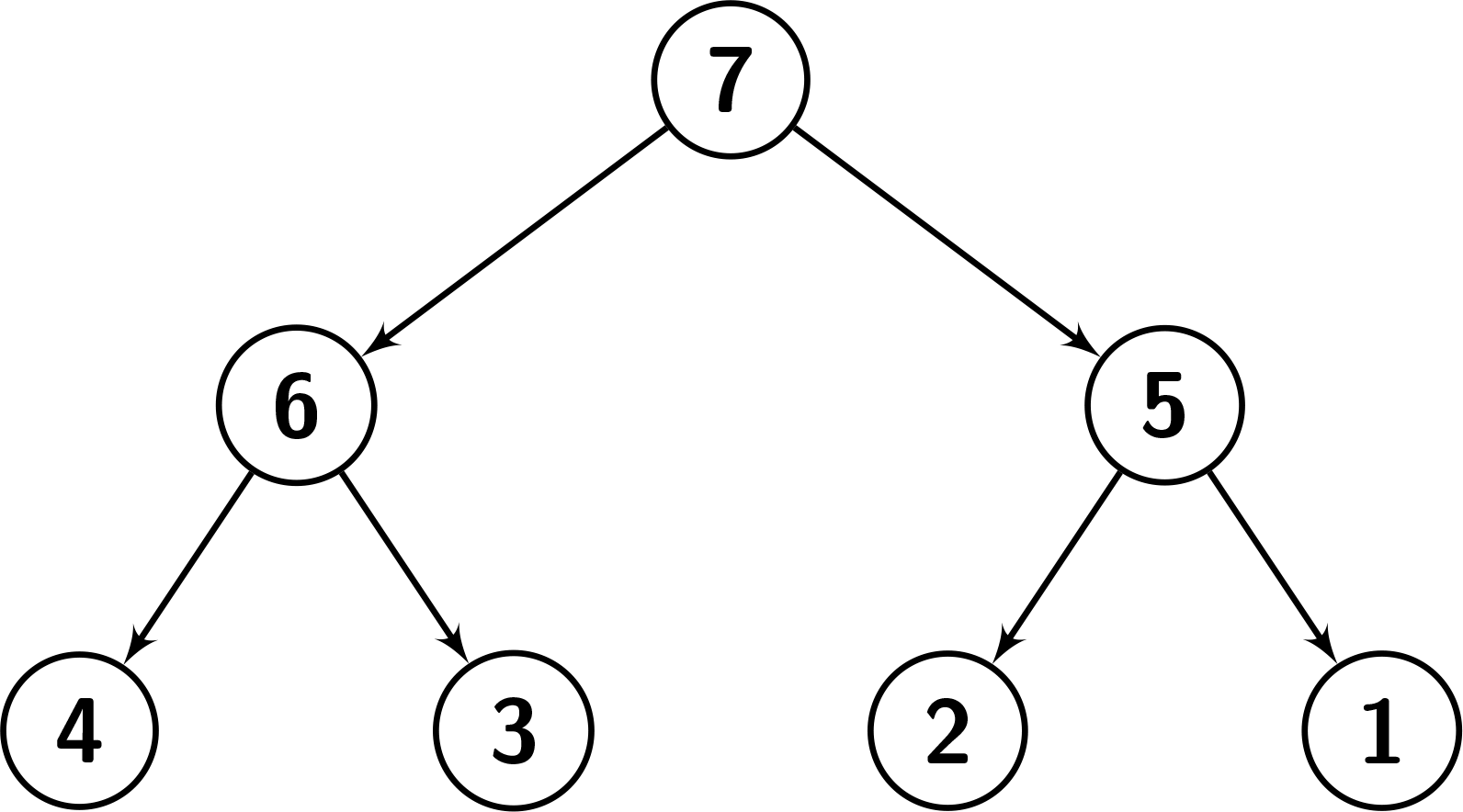
Example 2:

Input: root = [1,2,3], k = 1
Output: 0
Explanation: Number the nodes from 1 to 3.
The values in the subtree of node 1: {1,2,3}. Since node.val == 1, there are no nodes having a smaller value than its value. So it's not great enough.
The values in the subtree of node 2: {2}. Since node.val == 2, there are no nodes having a smaller value than its value. So it's not great enough.
The values in the subtree of node 3: {3}. Since node.val == 3, there are no nodes having a smaller value than its value. So it's not great enough.
See the picture below for a better understanding.

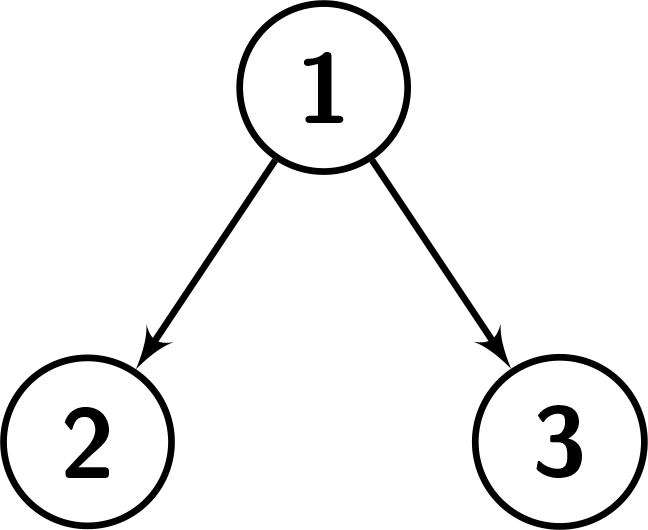
Example 3:

Input: root = [3,2,2], k = 2
Output: 1
Explanation: Number the nodes from 1 to 3.
The values in the subtree of node 1: {2,2,3}. Since node.val == 3, there are 2 nodes having a smaller value than its value. So it's great enough.
The values in the subtree of node 2: {2}. Since node.val == 2, there are no nodes having a smaller value than its value. So it's not great enough.
The values in the subtree of node 3: {2}. Since node.val == 2, there are no nodes having a smaller value than its value. So it's not great enough.
See the picture below for a better understanding.

 

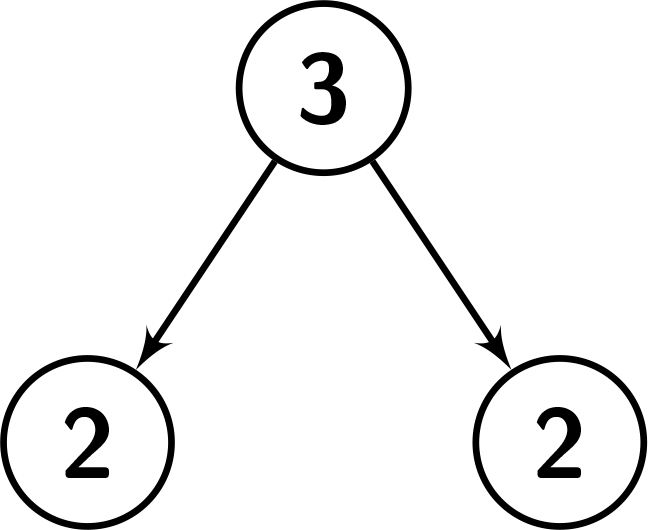
Constraints:

• The number of nodes in the tree is in the range [1, 104].
• 1 <= Node.val <= 104
• 1 <= k <= 10

public int CountGreatEnoughNodes(TreeNode root, int k)
{
    int retVal = 0;
    List listSubtree = new List();
    CountGreatEnoughNodes(root, k, ref listSubtree, ref retVal);

    return retVal;
}

private void CountGreatEnoughNodes(TreeNode node,
                                    int k,
                                    ref List listSubtree,
                                    ref int retVal)
{
    if (node == null) return;

    List leftSubtree = new List();
    CountGreatEnoughNodes(node.left, k, ref leftSubtree, ref retVal);

    List rightSubtree = new List();
    CountGreatEnoughNodes(node.right, k, ref rightSubtree, ref retVal);

    listSubtree = MergeSortedLists(leftSubtree, rightSubtree, k);

    if (listSubtree.Count >= k && node.val > listSubtree[k - 1]) retVal++;

    AddToSortedList(node.val, ref listSubtree, k);
}

private List MergeSortedLists(List list1,
                                    List list2,
                                    int k)
{
    List retVal = new List();

    int index1 = 0;
    int index2 = 0;
    while (index1 < list1.Count &&
        index2 < list2.Count &&
        index1 + index2 < k)
    {
        if (list1[index1] < list2[index2])
        {
            retVal.Add(list1[index1]);
            index1++;
        }
        else
        {
            retVal.Add(list2[index2]);
            index2++;
        }
    }

    while (index1 < list1.Count && index1 + index2 < k)
    {
        retVal.Add(list1[index1]);
        index1++;
    }
    while (index2 < list2.Count && index1 + index2 < k)
    {
        retVal.Add(list2[index2]);
        index2++;
    }

    return retVal;
}

public void AddToSortedList(int val, ref List sortedList, int k)
{
    bool added = false;
    for (int i = 0; i < sortedList.Count; i++)
    {
        if (sortedList[i] > val)
        {
            sortedList.Insert(i, val);
            added = true;
            break;
        }
    }

    if (!added) sortedList.Add(val);

    if (sortedList.Count > k)
        sortedList.RemoveAt(k);
}