Very interesting Tree problem

This is one of the most interesting Tree problems that I have seen in a long time. In spite of the high number of thumbs down, I think this problem exercises multiple concepts of algorithms and data structures.

The first point is that it limits the number of nodes in the tree to a very small number (2^5 - 1). With that, at least in my solution, I start by creating the full complete tree. In the process of creating it, have a hash table mapping a key to each node. The key can be calculated as a unique function from {depth, position} to a node. To make it unique, just multiply depth by a large number, and add position.

Once you have the map, go thru the input and calculate the same key, find the node and assign the value.

At this point there is still a problem where there might be multiple unused nodes. Write a DFS function to remove the unused nodes.

Finally, create a function to calculate the sum of all paths, again using DFS.

Code is down below, Happy Holidays!!! ACC.

Path Sum IV - LeetCode

666. Path Sum IV

Medium

If the depth of a tree is smaller than 5, then this tree can be represented by an array of three-digit integers. For each integer in this array:

• The hundreds digit represents the depth d of this node where 1 <= d <= 4.
• The tens digit represents the position p of this node in the level it belongs to where 1 <= p <= 8. The position is the same as that in a full binary tree.
• The units digit represents the value v of this node where 0 <= v <= 9.

Given an array of ascending three-digit integers nums representing a binary tree with a depth smaller than 5, return the sum of all paths from the root towards the leaves.

It is guaranteed that the given array represents a valid connected binary tree.

 

Example 1:

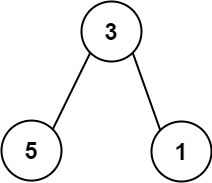
Input: nums = [113,215,221]
Output: 12
Explanation: The tree that the list represents is shown.
The path sum is (3 + 5) + (3 + 1) = 12.

Example 2:

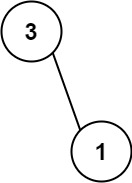
Input: nums = [113,221]
Output: 4
Explanation: The tree that the list represents is shown. 
The path sum is (3 + 1) = 4.

 

Constraints:

• 1 <= nums.length <= 15
• 110 <= nums[i] <= 489
• nums represents a valid binary tree with depth less than 5.

Accepted

27,433

Submissions

45,194

public class Solution {
    public class TreeNode
    {
        public int val;
        public TreeNode left;
        public TreeNode right;
        public TreeNode(int val = 0, TreeNode left = null, TreeNode right = null)
        {
            this.val = val;
            this.left = left;
            this.right = right;
        }
    }

    public int PathSum(int[] nums)
    {
        TreeNode tree = new TreeNode(-1);
        Hashtable map = new Hashtable();
        int[] currentPositionDepth = new int[5];
        for (int i = 0; i < 5; i++)
            currentPositionDepth[i] = 1;
        CreateTreeAndMap(map, tree, 1, currentPositionDepth);

        for (int i = 0; i < nums.Length; i++)
        {
            int depth = nums[i] / 100;
            int position = (nums[i] / 10) % 10;
            int value = nums[i] % 10;

            int key = depth * (100 + 7) + position;
            TreeNode node = (TreeNode)map[key];
            node.val = value;
        }

        DeleteUnusedNodes(tree);

        int retVal = 0;
        SumPaths(tree, 0, ref retVal);

        return retVal;
    }

    private void SumPaths(TreeNode node,
                          int currentPathSum,
                          ref int totalSum)
    {
        if (node == null) return;

        if (node.left == null && node.right == null)
        {
            totalSum += currentPathSum + node.val;
            return;
        }

        SumPaths(node.left, currentPathSum + node.val, ref totalSum);
        SumPaths(node.right, currentPathSum + node.val, ref totalSum);
    }

    private void DeleteUnusedNodes(TreeNode tree)
    {
        if (tree == null) return;

        if (tree.left != null)
        {
            if (tree.left.val != -1) DeleteUnusedNodes(tree.left);
            else tree.left = null;
        }
        if (tree.right != null)
        {
            if (tree.right.val != -1) DeleteUnusedNodes(tree.right);
            else tree.right = null;
        }
    }

    private void CreateTreeAndMap(Hashtable map,
                                  TreeNode node,
                                  int currentDepth,
                                  int[] currentPositionDepth)
    {
        int key = currentDepth * (100 + 7) + currentPositionDepth[currentDepth - 1];
        currentPositionDepth[currentDepth - 1]++;
        map.Add(key, node);

        if (currentDepth + 1 <= 5)
        {
            node.left = new TreeNode(-1);
            CreateTreeAndMap(map, node.left, currentDepth + 1, currentPositionDepth);
            node.right = new TreeNode(-1);
            CreateTreeAndMap(map, node.right, currentDepth + 1, currentPositionDepth);
        }
    }
}