Analysis: multiple for-loops still in constant time

This is an interesting problem: the key here is to keep track of the frequency within the Y, frequency outside of the Y, and then at this point we can try "all possibilities". But all possibilities here means actually a constant time. In the code below, you have 3*3*3 = 27 iterations. Just be careful when you see nested loops, they may still be cnstant time. Code is down below, cheers, ACC.

Minimum Operations to Write the Letter Y on a Grid - LeetCode

You are given a 0-indexed n x n grid where n is odd, and grid[r][c] is 0, 1, or 2.

We say that a cell belongs to the Letter Y if it belongs to one of the following:

• The diagonal starting at the top-left cell and ending at the center cell of the grid.
• The diagonal starting at the top-right cell and ending at the center cell of the grid.
• The vertical line starting at the center cell and ending at the bottom border of the grid.

The Letter Y is written on the grid if and only if:

• All values at cells belonging to the Y are equal.
• All values at cells not belonging to the Y are equal.
• The values at cells belonging to the Y are different from the values at cells not belonging to the Y.

Return the minimum number of operations needed to write the letter Y on the grid given that in one operation you can change the value at any cell to 0, 1, or 2.

 

Example 1:

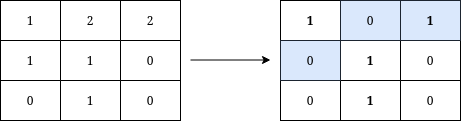
Input: grid = [[1,2,2],[1,1,0],[0,1,0]]
Output: 3
Explanation: We can write Y on the grid by applying the changes highlighted in blue in the image above. After the operations, all cells that belong to Y, denoted in bold, have the same value of 1 while those that do not belong to Y are equal to 0.
It can be shown that 3 is the minimum number of operations needed to write Y on the grid.

Example 2:

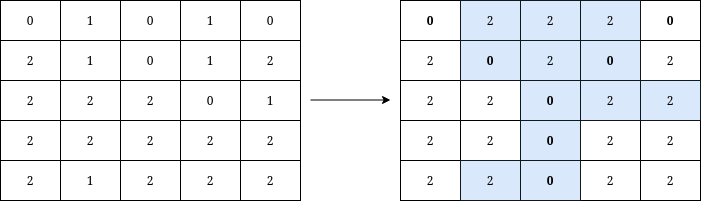
Input: grid = [[0,1,0,1,0],[2,1,0,1,2],[2,2,2,0,1],[2,2,2,2,2],[2,1,2,2,2]]
Output: 12
Explanation: We can write Y on the grid by applying the changes highlighted in blue in the image above. After the operations, all cells that belong to Y, denoted in bold, have the same value of 0 while those that do not belong to Y are equal to 2. 
It can be shown that 12 is the minimum number of operations needed to write Y on the grid.

 

Constraints:

• 3 <= n <= 49
• n == grid.length == grid[i].length
• 0 <= grid[i][j] <= 2
• n is odd.

    public int MinimumOperationsToWriteY(int[][] grid)
    {
        Hashtable freqInY = new Hashtable();
        Hashtable freqOutY = new Hashtable();

        FrequencyCountInY(grid, freqInY);
        FrequencyCountOutY(grid, freqOutY);

        int retVal = Int32.MaxValue;
        for (int inY = 0; inY <= 2; inY++)
        {
            for (int outY = 0; outY <= 2; outY++)
            {
                if (inY != outY)
                {
                    retVal = Math.Min(retVal, NumberOperationsInYOutY(freqInY, freqOutY, inY, outY));
                }
            }
        }

        return retVal;
    }

    private int NumberOperationsInYOutY(Hashtable freqInY, Hashtable freqOutY, int inY, int outY)
    {
        int numberInY = 0;
        foreach (int key in freqInY.Keys)
        {
            if (key != inY)
            {
                numberInY += (int)freqInY[key];
            }
        }

        int numberOutY = 0;
        foreach (int key in freqOutY.Keys)
        {
            if (key != outY)
            {
                numberOutY += (int)freqOutY[key];
            }
        }

        return numberInY + numberOutY;
    }

    private void FrequencyCountOutY(int[][] grid, Hashtable frequency)
    {
        for (int r = 0; r < grid.Length; r++)
        {
            for (int c = 0; c < grid[r].Length; c++)
            {
                if (grid[r][c] != -1)
                {
                    if (!frequency.ContainsKey(grid[r][c])) frequency.Add(grid[r][c], 0);
                    frequency[grid[r][c]] = (int)frequency[grid[r][c]] + 1;
                }
            }
        }
    }

    private void FrequencyCountInY(int[][] grid, Hashtable frequency)
    {
        int colLeft = 0;
        int colRight = grid[0].Length - 1;
        int row = 0;

        //Diagonals
        while (row < grid.Length / 2)
        {
            int[] numbers = { grid[row][colLeft], grid[row][colRight] };
            foreach (int n in numbers)
            {
                if (!frequency.ContainsKey(n)) frequency.Add(n, 0);
                frequency[n] = (int)frequency[n] + 1;
            }
            grid[row][colLeft] = -1;
            grid[row][colRight] = -1;
            colLeft++;
            colRight--;
            row++;
        }

        //Center
        for (int r = grid.Length / 2; r < grid.Length; r++)
        {
            int[] numbers = { grid[r][grid[r].Length / 2] };
            foreach (int n in numbers)
            {
                if (!frequency.ContainsKey(n)) frequency.Add(n, 0);
                frequency[n] = (int)frequency[n] + 1;
            }
            grid[r][grid[r].Length / 2] = -1;
        }
    }