Prefix Sum VI: DP-like solution

You can think of the solution to this problem in two ways: either a prefix sum, or a Dynamic Programming where you're solving the problem for the {r-1, c}, {r, c-1} and {r-1,c-1} and using those solutions to solve the problem for {r,c}. Code is down below, cheers, ACC.

Count Submatrices With Equal Frequency of X and Y - LeetCode

3212. Count Submatrices With Equal Frequency of X and Y

Medium

Given a 2D character matrix grid, where grid[i][j] is either 'X', 'Y', or '.', return the number of submatrices that contains:

• grid[0][0]
• an equal frequency of 'X' and 'Y'.
• at least one 'X'.

 

Example 1:

Input: grid = [["X","Y","."],["Y",".","."]]

Output: 3

Explanation:

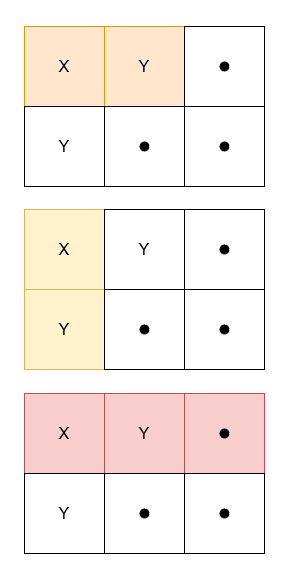
Example 2:

Input: grid = [["X","X"],["X","Y"]]

Output: 0

Explanation:

No submatrix has an equal frequency of 'X' and 'Y'.

Example 3:

Input: grid = [[".","."],[".","."]]

Output: 0

Explanation:

No submatrix has at least one 'X'.

 

Constraints:

• 1 <= grid.length, grid[i].length <= 1000
• grid[i][j] is either 'X', 'Y', or '.'.

public class Solution {
    public class CellXY
    {
        public int x = 0;
        public int y = 0;
    }

    public int NumberOfSubmatrices(char[][] grid)
    {
        CellXY[][] cellXY = new CellXY[grid.Length][];
        for (int r = 0; r < grid.Length; r++) cellXY[r] = new CellXY[grid[r].Length];

        cellXY[0][0] = new CellXY();
        cellXY[0][0].x = (grid[0][0] == 'X') ? 1 : 0;
        cellXY[0][0].y = (grid[0][0] == 'Y') ? 1 : 0;

        int retVal = 0;
        for (int r = 0; r < grid.Length; r++)
        {
            for (int c = 0; c < grid[r].Length; c++)
            {
                if (r == 0 && c == 0) continue;
                cellXY[r][c] = new CellXY();
                cellXY[r][c].x = (grid[r][c] == 'X') ? 1 : 0;
                cellXY[r][c].y = (grid[r][c] == 'Y') ? 1 : 0;

                if (r - 1 >= 0)
                {
                    cellXY[r][c].x += cellXY[r - 1][c].x;
                    cellXY[r][c].y += cellXY[r - 1][c].y;
                }
                if (c - 1 >= 0)
                {
                    cellXY[r][c].x += cellXY[r][c - 1].x;
                    cellXY[r][c].y += cellXY[r][c - 1].y;
                }
                if (r - 1 >= 0 && c - 1 >= 0)
                {
                    cellXY[r][c].x -= cellXY[r - 1][c - 1].x;
                    cellXY[r][c].y -= cellXY[r - 1][c - 1].y;
                }

                if (cellXY[r][c].x > 0 && cellXY[r][c].x == cellXY[r][c].y) retVal++;
            }
        }

        return retVal;
    }
}