Prefix Sum VIII

In this example a simple prefix sum approach does the job. Some caveats to keep in mind. First, there is no reason to use a hash table - in this case two simple prefix sum arrays work. Second, watch for overflow, since you're going to be adding up numbers that can grow up to 10^10, use long instead of int. Finally, the calculation of prefix sum is usually straightforward, following the pattern:

PrefixSum[i] == PrefixSum[Last] - PrefixSum[i]

Code is down below, cheers, keep coding.
ACC

Equal Sum Grid Partition I - LeetCode

You are given an m x n matrix grid of positive integers. Your task is to determine if it is possible to make either one horizontal or one vertical cut on the grid such that:

• Each of the two resulting sections formed by the cut is non-empty.
• The sum of the elements in both sections is equal.

Return true if such a partition exists; otherwise return false.

 

Example 1:

Input: grid = [[1,4],[2,3]]

Output: true

Explanation:

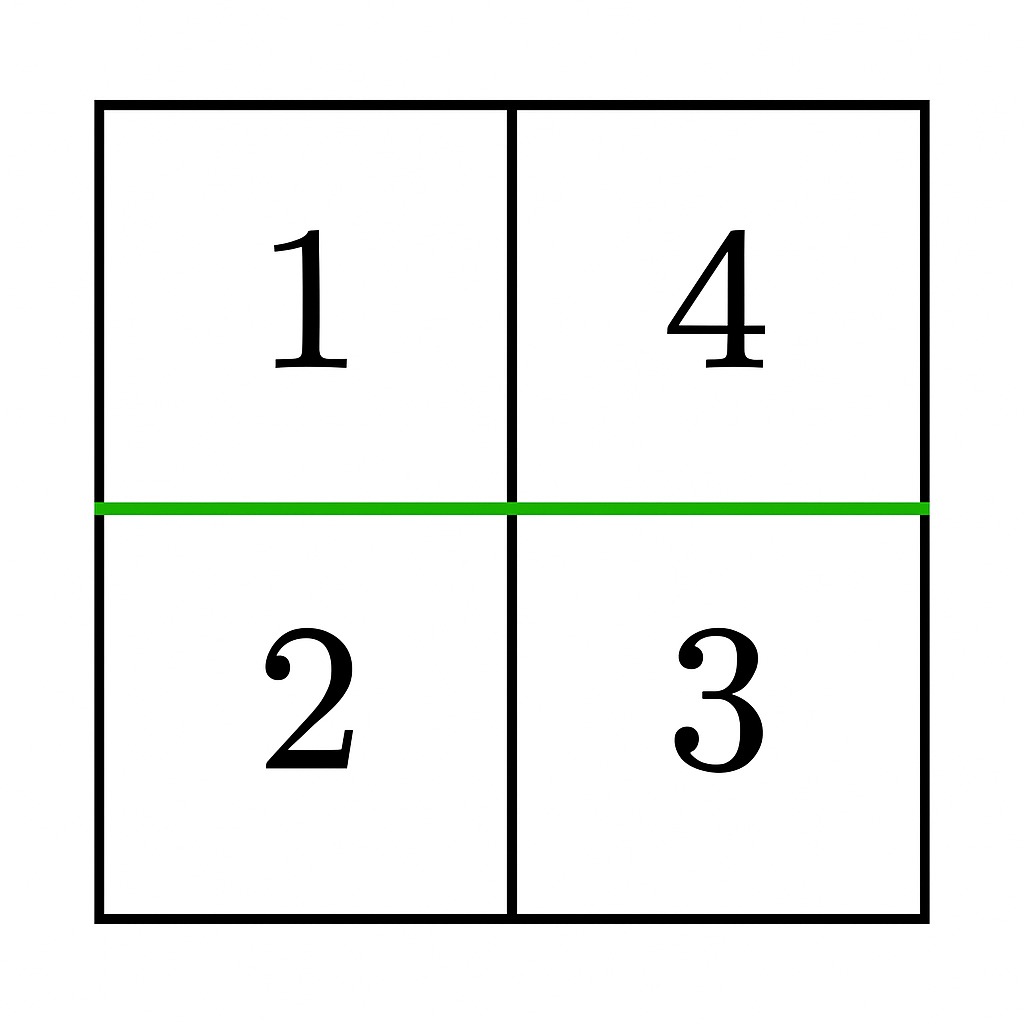
A horizontal cut between row 0 and row 1 results in two non-empty sections, each with a sum of 5. Thus, the answer is true.

Example 2:

Input: grid = [[1,3],[2,4]]

Output: false

Explanation:

No horizontal or vertical cut results in two non-empty sections with equal sums. Thus, the answer is false.

 

Constraints:

• 1 <= m == grid.length <= 105
• 1 <= n == grid[i].length <= 105
• 2 <= m * n <= 105
• 1 <= grid[i][j] <= 105

public bool CanPartitionGrid(int[][] grid)
{
    long[] rowsPrefixSum = new long[grid.Length];
    long[] colsPrefixSum = new long[grid[0].Length];

    for (int row = 0; row < grid.Length; row++)
    {
        for (int col = 0; col < grid[row].Length; col++)
        {
            rowsPrefixSum[row] += grid[row][col];
            colsPrefixSum[col] += grid[row][col];
        }
    }

    //Prefix sum
    for (int i = 1; i < rowsPrefixSum.Length; i++)
        rowsPrefixSum[i] += rowsPrefixSum[i - 1];
    for (int i = 1; i < colsPrefixSum.Length; i++)
        colsPrefixSum[i] += colsPrefixSum[i - 1];

    //Process
    for (int i = 0; i < rowsPrefixSum.Length - 1; i++)
    {
        if (rowsPrefixSum[i] == rowsPrefixSum[rowsPrefixSum.Length - 1] - rowsPrefixSum[i])
            return true;
    }
    for (int i = 0; i < colsPrefixSum.Length - 1; i++)
    {
        if (colsPrefixSum[i] == colsPrefixSum[colsPrefixSum.Length - 1] - colsPrefixSum[i])
            return true;
    }

    return false;
}