Techniques to facilitate a Breadth-First-Search (BFS)

Today's problem is this, from Daily Coding Problem:

Good morning! Here's your coding interview problem for today.

This problem was asked by Google.

You are given an M by N matrix consisting of booleans that represents a board. Each True boolean represents a wall. Each False boolean represents a tile you can walk on.

Given this matrix, a start coordinate, and an end coordinate, return the minimum number of steps required to reach the end coordinate from the start. If there is no possible path, then return null. You can move up, left, down, and right. You cannot move through walls. You cannot wrap around the edges of the board.

For example, given the following board:

[[f, f, f, f],
[t, t, f, t],
[f, f, f, f],
[f, f, f, f]]

and start = (3, 0) (bottom left) and end = (0, 0) (top left), the minimum number of steps required to reach the end is 7, since we would need to go through (1, 2) because there is a wall everywhere else on the second row.

The way to solve is by doing a Breadth-First-Search (BFS) and using some helper methods and techniques along the way:

• Try to use a Queue data structure provided by your favorite programming language
• Create a class or struct to hold the object to be enqueued - this is important if you also want to print the path from start to end, and not only the number of steps
• Use a hash-table to keep track of  which cells have already been visited. You can use some math techniques to figure out the key given the row and column indexes
• Create a helper method to determine whether the cell is walk-able

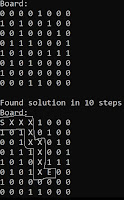
And few more minor things. Other than that, standard BFS. Here is an example of what the code outputs. Code's been checked-in on GitHub here: https://github.com/marcelodebarros/dailycodingproblem/blob/master/DailyCodingProblem10072018.cs

Cheers, Marcelo

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Collections;

namespace DailyCodingProblem
{
 class DailyCodingProblem10072018
 {
  private char[][] board = null;
  private int M;
  private int N;

  public DailyCodingProblem10072018(int M, int N)
  {
   this.M = M;
   this.N = N;
   board = new char[this.M][];

   Random rd = new Random();
   for (int r = 0; r < this.M; r++)
   {
    board[r] = new char[this.N];
    for (int c = 0; c < this.N; c++)
    {
     board[r][c] = rd.Next(0, 10) <= 3 ? '1' : '0';
    }
   }

   PrintBoard();
  }

  public void Walk(int ir, int ic, int er, int ec)
  {
   if (!CanWalkOn(ir, ic))
   {
    Console.WriteLine("No valid path found");
    return;
   }

   Queue queue = new Queue();
   Hashtable visited = new Hashtable();
   BoardItem bi = new BoardItem(ir, ic, 0, null);
   queue.Enqueue(bi);
   visited.Add(Key(ir, ic), true);

   bool foundSolution = false;
   while (queue.Count > 0)
   {
    BoardItem currentBoardItem = (BoardItem)queue.Dequeue();

    if (currentBoardItem.r == er && currentBoardItem.c == ec)
    {
     AddPathToBoard(currentBoardItem, ir, ic, er, ec);
     Console.WriteLine("Found solution in {0} steps", currentBoardItem.nSteps);
     PrintBoard();
     foundSolution = true;
     break;
    }

    int[] delta = { -1, 0, 1, 0, 0, -1, 0, 1 };

    for (int d = 0; d < delta.Length - 1; d += 2)
    {
     int nr = currentBoardItem.r + delta[d];
     int nc = currentBoardItem.c + delta[d + 1];
     long key = Key(nr, nc);
     if (CanWalkOn(nr, nc) && !visited.ContainsKey(key))
     {
      visited.Add(key, true);
      BoardItem newBoardItem = new BoardItem(nr, nc, currentBoardItem.nSteps + 1, currentBoardItem);
      queue.Enqueue(newBoardItem);
     }
    }
   }

   if (!foundSolution)
   {
    Console.WriteLine("No valid path found");
   }
  }

  private void AddPathToBoard(BoardItem bi, int ir, int ic, int er, int ec)
  {
   if (bi == null) return;
   if (bi.r == ir && bi.c == ic) board[bi.r][bi.c] = 'S';
   else if (bi.r == er && bi.c == ec) board[bi.r][bi.c] = 'E';
   else board[bi.r][bi.c] = 'X';
   AddPathToBoard(bi.previousItem, ir, ic, er, ec);
  }

  private void PrintBoard()
  {
   Console.WriteLine("Board:");
   for (int r = 0; r < M; r++)
   {
    for (int c = 0; c < N; c++)
    {
     Console.Write("{0} ", board[r][c]);
    }
    Console.WriteLine();
   }
   Console.WriteLine();
  }

  private bool CanWalkOn(int r, int c)
  {
   return r >= 0 &&
       r < M &&
       c >= 0 &&
       c < N &&
       board[r][c] == '0';
  }

  private long Key(int r, int c)
  {
   long rl = (long)r;
   long rc = (long)c;
   return rl * M * N + rc;
  }
 }

 class BoardItem
 {
  public int r;
  public int c;
  public int nSteps;
  public BoardItem previousItem;

  public BoardItem(int r, int c, int nSteps, BoardItem previousItem)
  {
   this.r = r;
   this.c = c;
   this.nSteps = nSteps;
   this.previousItem = previousItem;
  }
 }
}