Completeness of a Binary Tree, by LeetCode
This was one of the most interesting problems I've seen recently, comes from LeetCode, here it is its description: https://leetcode.com/problems/check-completeness-of-a-binary-tree/description/


I thought for a while and after going thru all the portfolio of tree processing techniques (DFS, BFS, balancing algorithms, etc.), I settled on a technique that we usually learn when we're building a Heap. When we build a (binary) heap, usually we use an array and each node N of the heap has children at positions 2N and 2N+1. Hence we could flatten the tree into an array of fixed size (N=100, hence O(1)-space) by filling it out (using any traversal: in-order, pre-order or post-order. I did it using the latter) using the rule that any node "i" has its children at positions 2i and 2i+1. And if the tree is complete as defined above, at the end that array will be "compact": the first part filled up with valid nodes, second one filled up with no nodes.
The image below exemplifies the idea. Notice that the complete tree has no gaps, whereas the incomplete one does:
The array as mentioned before has fixed size (N=100), hence O(1)-space. Notice that if the limit has not been given, then you'd then count the number of nodes and create an array of that size, in which case this would be an O(n)-space.
The traversal to fill out the array is an O(n)-time, and the check of compactness of the array is also an easy O(n)-time.
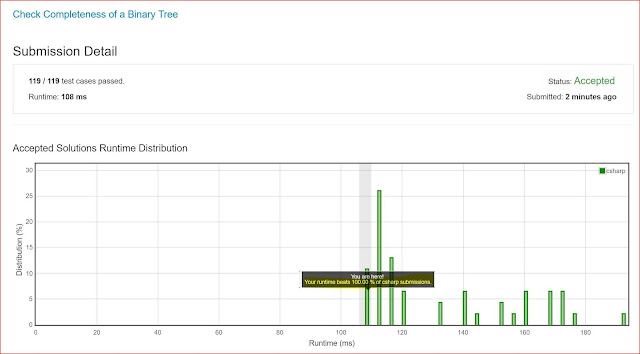
Hence, the algorithm runs in O(n)-time and O(1)-space, where n = number of nodes in the tree. Fast enough to beat all the other C# submissions. Code is down below, cheers, Marcelo.
Given a binary tree, determine if it is a complete binary tree.
Definition of a complete binary tree from Wikipedia:
In a complete binary tree every level, except possibly the last, is completely filled, and all nodes in the last level are as far left as possible. It can have between 1 and 2h nodes inclusive at the last level h.
In a complete binary tree every level, except possibly the last, is completely filled, and all nodes in the last level are as far left as possible. It can have between 1 and 2h nodes inclusive at the last level h.
Example 1:

Input: [1,2,3,4,5,6] Output: true Explanation: Every level before the last is full (ie. levels with node-values {1} and {2, 3}), and all nodes in the last level ({4, 5, 6}) are as far left as possible.
Example 2:

Input: [1,2,3,4,5,null,7] Output: false Explanation: The node with value 7 isn't as far left as possible.
Note:
- The tree will have between 1 and 100 nodes.
I thought for a while and after going thru all the portfolio of tree processing techniques (DFS, BFS, balancing algorithms, etc.), I settled on a technique that we usually learn when we're building a Heap. When we build a (binary) heap, usually we use an array and each node N of the heap has children at positions 2N and 2N+1. Hence we could flatten the tree into an array of fixed size (N=100, hence O(1)-space) by filling it out (using any traversal: in-order, pre-order or post-order. I did it using the latter) using the rule that any node "i" has its children at positions 2i and 2i+1. And if the tree is complete as defined above, at the end that array will be "compact": the first part filled up with valid nodes, second one filled up with no nodes.
The image below exemplifies the idea. Notice that the complete tree has no gaps, whereas the incomplete one does:
The array as mentioned before has fixed size (N=100), hence O(1)-space. Notice that if the limit has not been given, then you'd then count the number of nodes and create an array of that size, in which case this would be an O(n)-space.
The traversal to fill out the array is an O(n)-time, and the check of compactness of the array is also an easy O(n)-time.
Hence, the algorithm runs in O(n)-time and O(1)-space, where n = number of nodes in the tree. Fast enough to beat all the other C# submissions. Code is down below, cheers, Marcelo.
public class Solution
{
public bool IsCompleteTree(TreeNode root)
{
int N = 100;
bool[] map = new bool[N + 1];
FillMap(root, ref map, 1);
int index = 1;
while (index < map.Length && map[index++]) ;
while (index < map.Length && !map[index++]) ;
return index == map.Length;
}
private void FillMap(TreeNode root, ref bool[] map, int index)
{
if (root == null) return;
FillMap(root.left, ref map, 2 * index);
FillMap(root.right, ref map, 2 * index + 1);
if (index >= 0 && index < map.Length) map[index] = true;
}
}




ReplyDeleteThank you for sharing.
Your solution will be perfect one since it is much easy to write compared to my solution written in last week Leetcode contest 115.
But I played with different ideas based on your approach, and the map using size N = 100 is very challenging one. I came cross the index out of range error. I did not fully understand the given condition of 100 nodes at most in the tree, if it is a complete tree, then map should be fit into 101. Otherwise, the size can be 1 + 2 + ...+ 2^100.
I spent time to learn your idea and play with different approach. None of them works and I could not make any improvement, so I tried to make a minor change to entertain the hard work and things I learned.
public class Solution {
public bool IsCompleteTree(TreeNode root)
{
int sum = 0;
int nodeCount = 0;
FillMap(root, 1, ref sum, ref nodeCount);
return sum == nodeCount * (nodeCount + 1)/2;
}
private static void FillMap(TreeNode root, int index, ref int sum, ref int nodeCount)
{
if (root == null)
{
return;
}
FillMap(root.left, 2 * index, ref sum, ref nodeCount);
FillMap(root.right, 2 * index + 1, ref sum, ref nodeCount);
sum += index;
nodeCount++;
}
}
I chose not to use map instead, I choose to use two variables to help me track, count of nodes in the tree and sum of index. The code passed Leetcode online judge. You give us a lot of inspiration I am talking from weekly contest players viewpoints.
Wow that’s an even more efficient solution!!!! Love it!!! Thx for sharing it!
ReplyDelete