Grid - Breadth First Search (BFS)

Although this is a typical BFS problem, it does require close attention to details. Here it is: https://leetcode.com/problems/check-if-there-is-a-valid-path-in-a-grid/

1391. Check if There is a Valid Path in a Grid

Medium

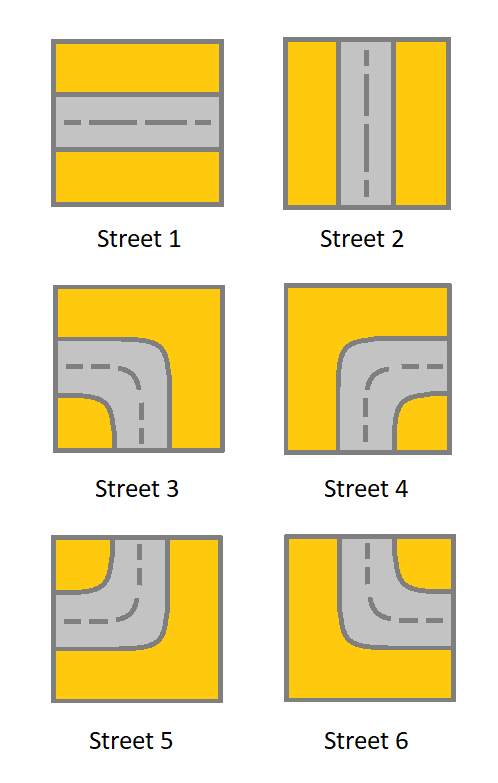
Given a m x n grid. Each cell of the grid represents a street. The street of grid[i][j] can be:

• 1 which means a street connecting the left cell and the right cell.
• 2 which means a street connecting the upper cell and the lower cell.
• 3 which means a street connecting the left cell and the lower cell.
• 4 which means a street connecting the right cell and the lower cell.
• 5 which means a street connecting the left cell and the upper cell.
• 6 which means a street connecting the right cell and the upper cell.

You will initially start at the street of the upper-left cell (0,0). A valid path in the grid is a path which starts from the upper left cell (0,0) and ends at the bottom-right cell (m - 1, n - 1). The path should only follow the streets.

Notice that you are not allowed to change any street.

Return true if there is a valid path in the grid or false otherwise.

Example 1:

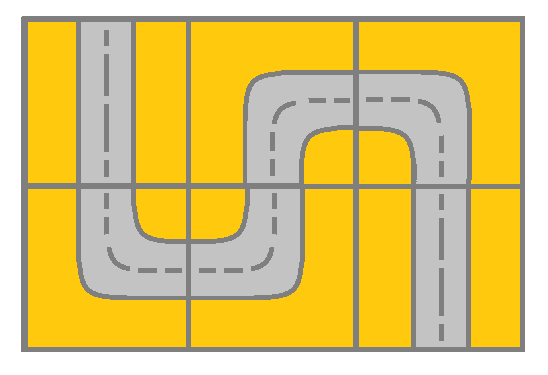
Input: grid = [[2,4,3],[6,5,2]]
Output: true
Explanation: As shown you can start at cell (0, 0) and visit all the cells of the grid to reach (m - 1, n - 1).

Example 2:

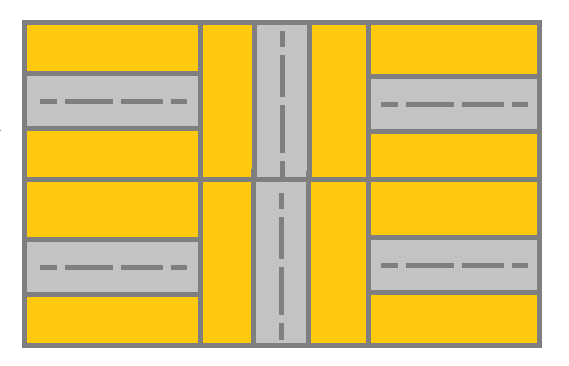
Input: grid = [[1,2,1],[1,2,1]]
Output: false
Explanation: As shown you the street at cell (0, 0) is not connected with any street of any other cell and you will get stuck at cell (0, 0)

Example 3:

Input: grid = [[1,1,2]]
Output: false
Explanation: You will get stuck at cell (0, 1) and you cannot reach cell (0, 2).

Example 4:

Input: grid = [[1,1,1,1,1,1,3]]
Output: true

Example 5:

Input: grid = [[2],[2],[2],[2],[2],[2],[6]]
Output: true

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 300
• 1 <= grid[i][j] <= 6

The important aspect to address is to understand the connection between the cells. There is quite a few combinations, around 6 x 2 x 3 or 36 which need to be coded properly (each one) otherwise few cases will fail. Other than that, straightforward BFS. Cheers, ACC.

public class Solution
{
    public bool HasValidPath(int[][] grid)
    {
        Hashtable visited = new Hashtable();
        Queue<QueueItem> queue = new Queue<QueueItem>();

        QueueItem qi = new QueueItem(0, 0);
        queue.Enqueue(qi);
        visited.Add(qi.key, true);

        while (queue.Count > 0)
        {
            QueueItem current = queue.Dequeue();

            if (current.row == grid.Length - 1 && current.col == grid[0].Length - 1) return true;

            int[] rowDelta = { 1, -1, 0, 0 };
            int[] colDelta = { 0, 0, 1, -1 };

            for (int i = 0; i < rowDelta.Length; i++)
            {
                int nRow = current.row + rowDelta[i];
                int nCol = current.col + colDelta[i];

                switch (grid[current.row][current.col])
                {
                    case 1:
                        if (nCol == current.col + 1 &&
                            nCol < grid[0].Length &&
                            (grid[nRow][nCol] == 1 || grid[nRow][nCol] == 3 || grid[nRow][nCol] == 5))
                        {
                            AddToQueue(queue, grid, nRow, nCol, visited);
                        }
                        if (nCol == current.col - 1 &&
                            nCol >= 0 &&
                            (grid[nRow][nCol] == 1 || grid[nRow][nCol] == 4 || grid[nRow][nCol] == 6))
                        {
                            AddToQueue(queue, grid, nRow, nCol, visited);
                        }
                        break;
                    case 2:
                        if (nRow == current.row + 1 &&
                            nRow < grid.Length &&
                            (grid[nRow][nCol] == 2 || grid[nRow][nCol] == 5 || grid[nRow][nCol] == 6))
                        {
                            AddToQueue(queue, grid, nRow, nCol, visited);
                        }
                        if (nRow == current.row - 1 &&
                            nRow >= 0 &&
                            (grid[nRow][nCol] == 2 || grid[nRow][nCol] == 3 || grid[nRow][nCol] == 4))
                        {
                            AddToQueue(queue, grid, nRow, nCol, visited);
                        }
                        break;
                    case 3:
                        if (nCol == current.col - 1 &&
                            nCol >= 0 &&
                            (grid[nRow][nCol] == 1 || grid[nRow][nCol] == 4 || grid[nRow][nCol] == 6))
                        {
                            AddToQueue(queue, grid, nRow, nCol, visited);
                        }
                        if (nRow == current.row + 1 &&
                            nRow < grid.Length &&
                            (grid[nRow][nCol] == 2 || grid[nRow][nCol] == 5 || grid[nRow][nCol] == 6))
                        {
                            AddToQueue(queue, grid, nRow, nCol, visited);
                        }
                        break;
                    case 4:
                        if (nCol == current.col + 1 &&
                            nCol < grid[0].Length &&
                            (grid[nRow][nCol] == 1 || grid[nRow][nCol] == 3 || grid[nRow][nCol] == 5))
                        {
                            AddToQueue(queue, grid, nRow, nCol, visited);
                        }
                        if (nRow == current.row + 1 &&
                            nRow < grid.Length &&
                            (grid[nRow][nCol] == 2 || grid[nRow][nCol] == 5 || grid[nRow][nCol] == 6))
                        {
                            AddToQueue(queue, grid, nRow, nCol, visited);
                        }
                        break;
                    case 5:
                        if (nCol == current.col - 1 &&
                            nCol >= 0 &&
                            (grid[nRow][nCol] == 1 || grid[nRow][nCol] == 4 || grid[nRow][nCol] == 6))
                        {
                            AddToQueue(queue, grid, nRow, nCol, visited);
                        }
                        if (nRow == current.row - 1 &&
                            nRow >= 0 &&
                            (grid[nRow][nCol] == 2 || grid[nRow][nCol] == 3 || grid[nRow][nCol] == 4))
                        {
                            AddToQueue(queue, grid, nRow, nCol, visited);
                        }
                        break;
                    case 6:
                        if (nCol == current.col + 1 &&
                            nCol < grid[0].Length &&
                            (grid[nRow][nCol] == 1 || grid[nRow][nCol] == 3 || grid[nRow][nCol] == 5))
                        {
                            AddToQueue(queue, grid, nRow, nCol, visited);
                        }
                        if (nRow == current.row - 1 &&
                            nRow >= 0 &&
                            (grid[nRow][nCol] == 2 || grid[nRow][nCol] == 3 || grid[nRow][nCol] == 4))
                        {
                            AddToQueue(queue, grid, nRow, nCol, visited);
                        }
                        break;
                }
            }
        }

        return false;
    }

    private void AddToQueue(Queue<QueueItem> queue,
                            int[][] grid,
                            int row,
                            int col,
                            Hashtable visited)
    {
        QueueItem nqi = new QueueItem(row, col);

        if (row >= 0 &&
            row < grid.Length &&
            col >= 0 &&
            col < grid[0].Length &&
            !visited.ContainsKey(nqi.key))
        {
            queue.Enqueue(nqi);
            visited.Add(nqi.key, true);
        }
    }
}

public class QueueItem
{
    public int row = 0;
    public int col = 0;
    public int key = 0;

    public QueueItem(int row, int col)
    {
        this.row = row;
        this.col = col;
        this.key = 400 * row + col;
    }
}