Hard BST Problem

Usually BST (Binary Search Tree) problems are not that hard, but this one is: https://leetcode.com/problems/maximum-sum-bst-in-binary-tree/

1373. Maximum Sum BST in Binary Tree

Hard

Given a binary tree root, the task is to return the maximum sum of all keys of any sub-tree which is also a Binary Search Tree (BST).

Assume a BST is defined as follows:

• The left subtree of a node contains only nodes with keys less than the node's key.
• The right subtree of a node contains only nodes with keys greater than the node's key.
• Both the left and right subtrees must also be binary search trees.

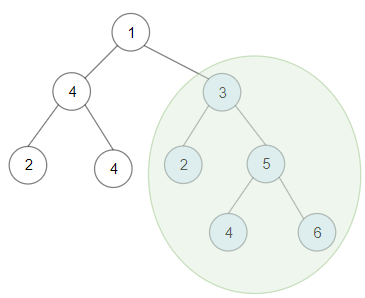
Example 1:

Input: root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6]
Output: 20
Explanation: Maximum sum in a valid Binary search tree is obtained in root node with key equal to 3.

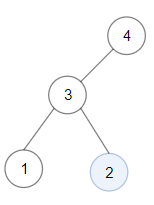
Example 2:

Input: root = [4,3,null,1,2]
Output: 2
Explanation: Maximum sum in a valid Binary search tree is obtained in a single root node with key equal to 2.

Example 3:

Input: root = [-4,-2,-5]
Output: 0
Explanation: All values are negatives. Return an empty BST.

Example 4:

Input: root = [2,1,3]
Output: 6

Example 5:

Input: root = [5,4,8,3,null,6,3]
Output: 7

Constraints:

• Each tree has at most 40000 nodes..
• Each node's value is between [-4 * 10^4 , 4 * 10^4]

The hint in the problem description gives you exactly what needs to be done. Here is the gist of it:
a) With 4 x 10^4 nodes, your solution will have to be either O(n) or O(nlogn). n^2 will timeout.
b) The node values are there just to specify the limits for the variables initialization
c) The solution that I came up with is O(n)
d) The solution is based on Post-Order Tree Traversal
e) The approach will be to check right, check left, and if both are valid BST, check for the possibility of a BST with the current node
f) Based on (e), update the max sum
g) Return the proper values for the current node (remember that the post-order traversal you process right, left then the current node)
h) Finally, be relentless and you'll succeed

Code is below, cheers, ACC.

public class Solution
{
    public int MaxSumBST(TreeNode root)
    {
        int maxVal = -100000;
        int minVal = 100000;
        int sumVal = 0;
        int retVal = Int32.MinValue;

        MaxSumBST(root, ref maxVal, ref minVal, ref sumVal, ref retVal);

        return retVal < 0 ? 0 : retVal;
    }

    private bool MaxSumBST(TreeNode node,
                            ref int maxVal,
                            ref int minVal,
                            ref int sumVal,
                            ref int maxSum)
    {
        if (node == null) return true;

        if (node.left == null && node.right == null) //Leaf
        {
            maxVal = node.val;
            minVal = node.val;
            sumVal = node.val;

            maxSum = Math.Max(sumVal, maxSum);

            return true;
        }

        int leftMaxVal = -100000;
        int leftMinVal = 100000;
        int leftSumVal = 0;
        bool isLeftBST = MaxSumBST(node.left, ref leftMaxVal, ref leftMinVal, ref leftSumVal, ref maxSum);

        int rightMaxVal = -100000;
        int rightMinVal = 100000;
        int rightSumVal = 0;
        bool isRightBST = MaxSumBST(node.right, ref rightMaxVal, ref rightMinVal, ref rightSumVal, ref maxSum);

        sumVal += leftSumVal + rightSumVal + node.val;
        maxVal = Math.Max(node.val, Math.Max(leftMaxVal, rightMaxVal));
        minVal = Math.Min(node.val, Math.Min(leftMinVal, rightMinVal));

        if (isLeftBST &&
            isRightBST &&
            (node.val > leftMaxVal || node.left == null) &&
            (node.val < rightMinVal || node.right == null))
        {
            maxSum = Math.Max(maxSum, sumVal);
            return true;
        }

        return false;
    }
}