Lattice points inside circles

Problem looks scarier than it actually is. There is a set of circles and you need to find the integer points within them. The caveat which is what makes this problem easy is that the number of points to cover is small, in the 0-100 range. Taking into account the radius too, you might want to extrapolate to -100 to 200, covering about 300 X's, 300 Y's and 200 circles, hence a total execution time of about 18M steps, which runs in a blink of an eye. Code below, cheers, ACC.

Count Lattice Points Inside a Circle - LeetCode

2249. Count Lattice Points Inside a Circle

Medium

Given a 2D integer array circles where circles[i] = [xi, yi, ri] represents the center (xi, yi) and radius ri of the ith circle drawn on a grid, return the number of lattice points that are present inside at least one circle.

Note:

• A lattice point is a point with integer coordinates.
• Points that lie on the circumference of a circle are also considered to be inside it.

 

Example 1:

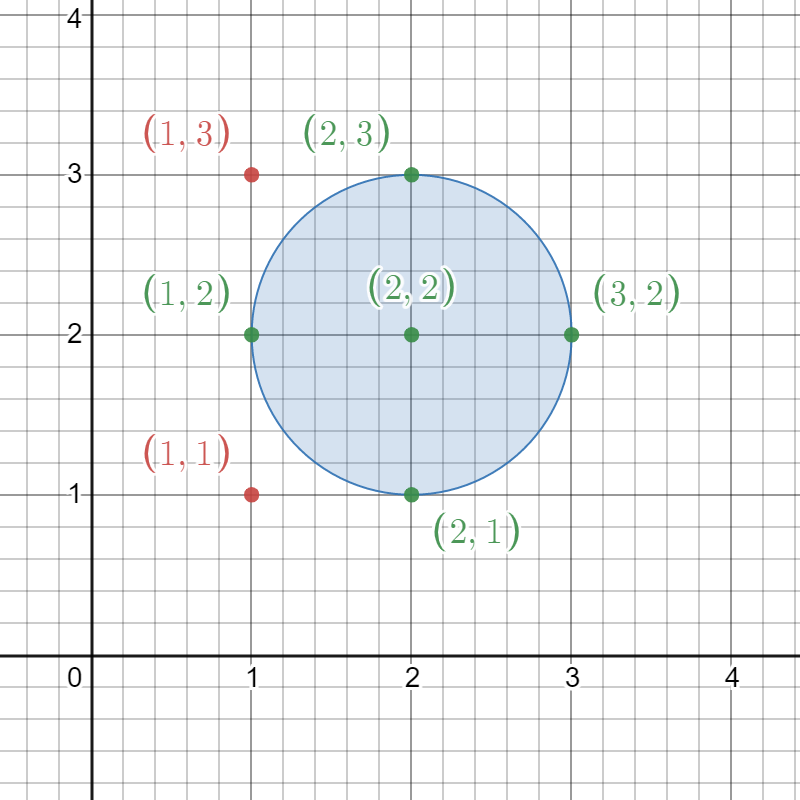
Input: circles = [[2,2,1]]
Output: 5
Explanation:
The figure above shows the given circle.
The lattice points present inside the circle are (1, 2), (2, 1), (2, 2), (2, 3), and (3, 2) and are shown in green.
Other points such as (1, 1) and (1, 3), which are shown in red, are not considered inside the circle.
Hence, the number of lattice points present inside at least one circle is 5.

Example 2:

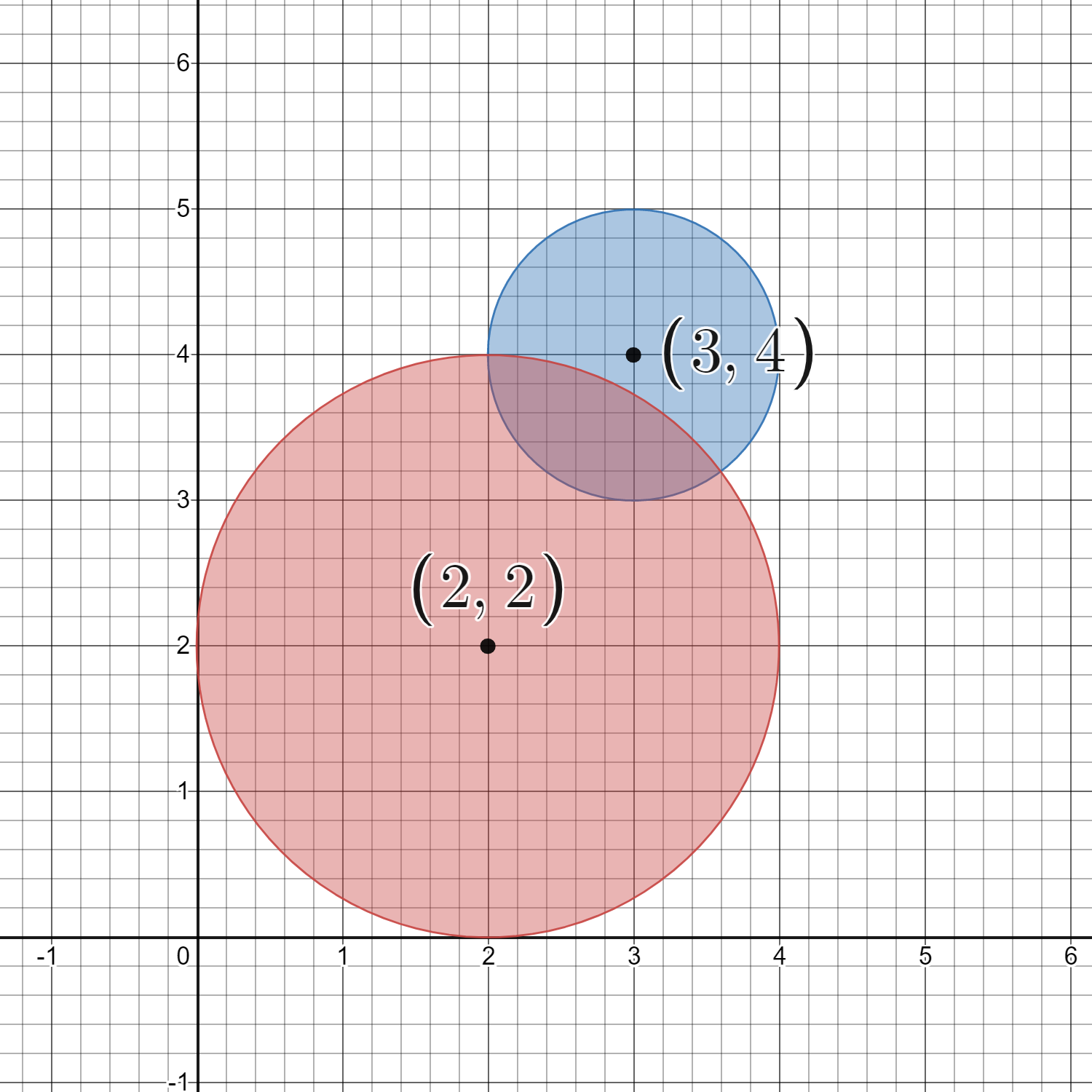
Input: circles = [[2,2,2],[3,4,1]]
Output: 16
Explanation:
The figure above shows the given circles.
There are exactly 16 lattice points which are present inside at least one circle. 
Some of them are (0, 2), (2, 0), (2, 4), (3, 2), and (4, 4).

 

Constraints:

• 1 <= circles.length <= 200
• circles[i].length == 3
• 1 <= xi, yi <= 100
• 1 <= ri <= min(xi, yi)

public class Solution {
    public int CountLatticePoints(int[][] circles)
    {
        int retVal = 0;
        for (int x = -100; x <= 200; x++)
        {
            for (int y = -100; y <= 200; y++)
            {
                bool found = false;
                foreach (int[] circle in circles)
                {
                    if ((x - circle[0]) * (x - circle[0]) + (y - circle[1]) * (y - circle[1]) <= circle[2] * circle[2])
                    {
                        found = true;
                        break;
                    }
                }
                if (found) retVal++;
            }
        }

        return retVal;
    }
}