Unguarded Cells: grid, hash and a linear approach

The problem this weekend asks for the number of cells that are not guarded. Since the limits of the grid are in the 10^5 range, we're then looking for a O(N) solution.

First, it would be wise to add the positions of the guards and the walls in handy hash-tables. Relatively simple.

After that, think this way: if you scan the grid in a left-to-right analyzing each row, you can increment the cells that are not reached by a guard in that row from left to right. Any cell that has a 1 at the end of this operation is free from guards in that row from left to right.

Now apply the same approach in the other 3 directions: right to left, top down and bottoms-up. By doing so, at the very end, any cell that reaches the number 4 is free from any guard. And that's your answer.

Thus, this would be a 4*m*n, and since m*n<=10^5 (as per the constraint), then the solution becomes O(4*10^5), which is very tractable and considered linear in this case. Code is down below, cheers, ACC.

Count Unguarded Cells in the Grid - LeetCode

2257. Count Unguarded Cells in the Grid

Medium

You are given two integers m and n representing a 0-indexed m x n grid. You are also given two 2D integer arrays guards and walls where guards[i] = [rowi, coli] and walls[j] = [rowj, colj] represent the positions of the ith guard and jth wall respectively.

A guard can see every cell in the four cardinal directions (north, east, south, or west) starting from their position unless obstructed by a wall or another guard. A cell is guarded if there is at least one guard that can see it.

Return the number of unoccupied cells that are not guarded.

 

Example 1:

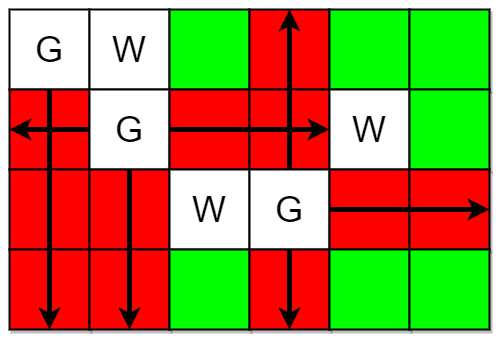
Input: m = 4, n = 6, guards = [[0,0],[1,1],[2,3]], walls = [[0,1],[2,2],[1,4]]
Output: 7
Explanation: The guarded and unguarded cells are shown in red and green respectively in the above diagram.
There are a total of 7 unguarded cells, so we return 7.

Example 2:

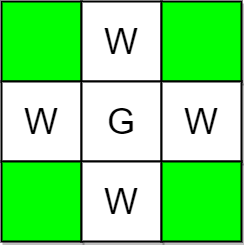
Input: m = 3, n = 3, guards = [[1,1]], walls = [[0,1],[1,0],[2,1],[1,2]]
Output: 4
Explanation: The unguarded cells are shown in green in the above diagram.
There are a total of 4 unguarded cells, so we return 4.

 

Constraints:

• 1 <= m, n <= 105
• 2 <= m * n <= 105
• 1 <= guards.length, walls.length <= 5 * 104
• 2 <= guards.length + walls.length <= m * n
• guards[i].length == walls[j].length == 2
• 0 <= rowi, rowj < m
• 0 <= coli, colj < n
• All the positions in guards and walls are unique.

public int CountUnguarded(int m, int n, int[][] guards, int[][] walls)
{
    int[][] count = new int[m][];
    for (int i = 0; i < count.Length; i++) count[i] = new int[n];

    Hashtable guardsHash = new Hashtable();
    for (int i = 0; i < guards.Length; i++)
    {
        long key = guards[i][0] * (100000 + 5) + guards[i][1];
        guardsHash.Add(key, true);
    }
    Hashtable wallsHash = new Hashtable();
    for (int i = 0; i < walls.Length; i++)
    {
        long key = walls[i][0] * (100000 + 5) + walls[i][1];
        wallsHash.Add(key, true);
    }

    //L->R
    for (int r = 0; r < m; r++)
    {
        bool lastIsGuard = false;
        for (int c = 0; c < n; c++)
        {
            long key = r * (100000 + 5) + c;
            if (guardsHash.ContainsKey(key))
            {
                lastIsGuard = true;
            }
            else if (wallsHash.ContainsKey(key))
            {
                lastIsGuard = false;
            }
            else if (!lastIsGuard)
            {
                count[r][c]++;
            }
        }
    }

    //R->L
    for (int r = 0; r < m; r++)
    {
        bool lastIsGuard = false;
        for (int c = n - 1; c >= 0; c--)
        {
            long key = r * (100000 + 5) + c;
            if (guardsHash.ContainsKey(key))
            {
                lastIsGuard = true;
            }
            else if (wallsHash.ContainsKey(key))
            {
                lastIsGuard = false;
            }
            else if (!lastIsGuard)
            {
                count[r][c]++;
            }
        }
    }

    //T->B
    for (int c = 0; c < n; c++)
    {
        bool lastIsGuard = false;
        for (int r = 0; r < m; r++)
        {
            long key = r * (100000 + 5) + c;
            if (guardsHash.ContainsKey(key))
            {
                lastIsGuard = true;
            }
            else if (wallsHash.ContainsKey(key))
            {
                lastIsGuard = false;
            }
            else if (!lastIsGuard)
            {
                count[r][c]++;
            }
        }
    }

    //B->T
    int retVal = 0;
    for (int c = 0; c < n; c++)
    {
        bool lastIsGuard = false;
        for (int r = m - 1; r >= 0; r--)
        {
            long key = r * (100000 + 5) + c;
            if (guardsHash.ContainsKey(key))
            {
                lastIsGuard = true;
            }
            else if (wallsHash.ContainsKey(key))
            {
                lastIsGuard = false;
            }
            else if (!lastIsGuard)
            {
                count[r][c]++;
                if (count[r][c] == 4) retVal++;
            }
        }
    }

    return retVal;
}