This is a Graph Problem - Not a Tree Problem!

Don't be fooled by the problem description! Although it does say "tree", what you really have here is a graph and you want to do a Depth First Search pruning based on the given restrictions. Graph can be coded using a Hashtable of Hashtables. Code is down below, cheers, ACC.

Reachable Nodes With Restrictions - LeetCode

2368. Reachable Nodes With Restrictions

Medium

There is an undirected tree with n nodes labeled from 0 to n - 1 and n - 1 edges.

You are given a 2D integer array edges of length n - 1 where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree. You are also given an integer array restricted which represents restricted nodes.

Return the maximum number of nodes you can reach from node 0 without visiting a restricted node.

Note that node 0 will not be a restricted node.

 

Example 1:

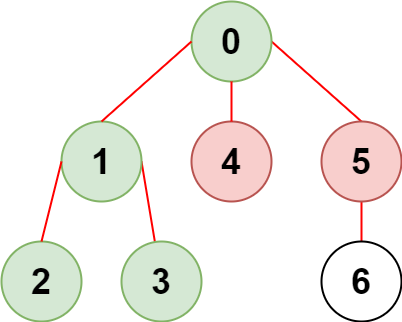
Input: n = 7, edges = [[0,1],[1,2],[3,1],[4,0],[0,5],[5,6]], restricted = [4,5]
Output: 4
Explanation: The diagram above shows the tree.
We have that [0,1,2,3] are the only nodes that can be reached from node 0 without visiting a restricted node.

Example 2:

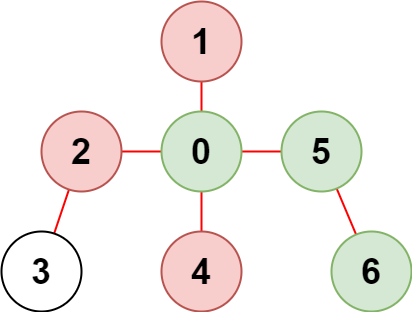
Input: n = 7, edges = [[0,1],[0,2],[0,5],[0,4],[3,2],[6,5]], restricted = [4,2,1]
Output: 3
Explanation: The diagram above shows the tree.
We have that [0,5,6] are the only nodes that can be reached from node 0 without visiting a restricted node.

 

Constraints:

• 2 <= n <= 105
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• edges represents a valid tree.
• 1 <= restricted.length < n
• 1 <= restricted[i] < n
• All the values of restricted are unique.

public int ReachableNodes(int n, int[][] edges, int[] restricted)
{
    Hashtable graph = new Hashtable();
    foreach (int[] edge in edges)
    {
        for (int i = 0; i < 2; i++)
        {
            if (!graph.ContainsKey(edge[i])) graph.Add(edge[i], new Hashtable());
            Hashtable connections = (Hashtable)graph[edge[i]];
            if (!connections.ContainsKey(edge[(i + 1) % 2])) connections.Add(edge[(i + 1) % 2], true);
        }
    }

    Hashtable restriction = new Hashtable();
    foreach (int r in restricted)
    {
        if (!restriction.ContainsKey(r)) restriction.Add(r, true);
    }

    int retVal = 0;
    Hashtable visited = new Hashtable();
    visited.Add(0, true);
    ReachableNodes(0, graph, visited, restriction, ref retVal);
    return retVal;
}

private void ReachableNodes(int node,
                            Hashtable graph,
                            Hashtable visited,
                            Hashtable restriction,
                            ref int maxReachableNodes)
{
    if (restriction.ContainsKey(node)) return;
    maxReachableNodes++;

    if (graph.ContainsKey(node))
    {
        Hashtable connections = (Hashtable)graph[node];
        foreach (int nextNode in connections.Keys)
        {
            if (!visited.ContainsKey(nextNode))
            {
                visited.Add(nextNode, true);
                ReachableNodes(nextNode, graph, visited, restriction, ref maxReachableNodes);
            }
        }
    }
}