This is a Graph Problem - Not a Tree Problem! Part II

Another deceiving problem: don't try to solve it as a Tree problem, you'll get stuck. Transform the tree into a graph first. Then, find the longest path starting from 'start' node, using DFS. Code is down below, cheers, ACC.

Amount of Time for Binary Tree to Be Infected - LeetCode

2385. Amount of Time for Binary Tree to Be Infected

Medium

You are given the root of a binary tree with unique values, and an integer start. At minute 0, an infection starts from the node with value start.

Each minute, a node becomes infected if:

• The node is currently uninfected.
• The node is adjacent to an infected node.

Return the number of minutes needed for the entire tree to be infected.

 

Example 1:

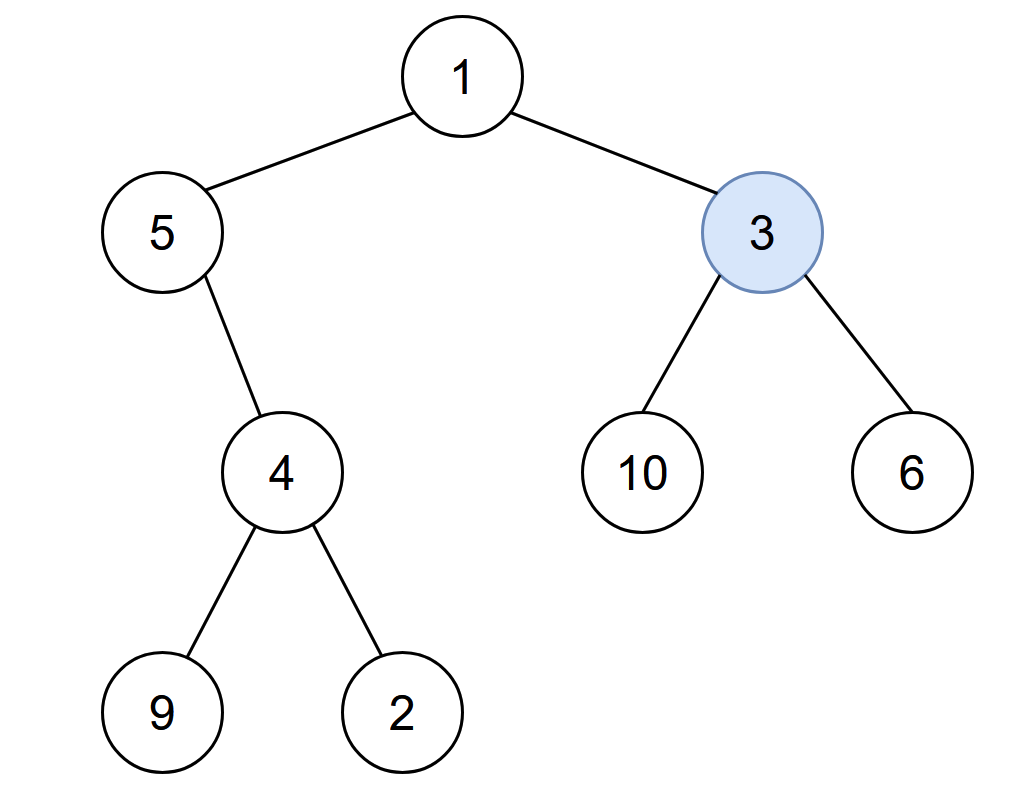
Input: root = [1,5,3,null,4,10,6,9,2], start = 3
Output: 4
Explanation: The following nodes are infected during:
- Minute 0: Node 3
- Minute 1: Nodes 1, 10 and 6
- Minute 2: Node 5
- Minute 3: Node 4
- Minute 4: Nodes 9 and 2
It takes 4 minutes for the whole tree to be infected so we return 4.

Example 2:

Input: root = [1], start = 1
Output: 0
Explanation: At minute 0, the only node in the tree is infected so we return 0.

 

Constraints:

• The number of nodes in the tree is in the range [1, 105].
• 1 <= Node.val <= 105
• Each node has a unique value.
• A node with a value of start exists in the tree.

public class Solution {
    public int AmountOfTime(TreeNode root, int start)
    {
        Hashtable graph = new Hashtable();

        Queue queue = new Queue();
        queue.Enqueue(root);
        while (queue.Count > 0)
        {
            TreeNode node = queue.Dequeue();
            if (!graph.ContainsKey(node.val)) graph.Add(node.val, new Hashtable());
            Hashtable children = (Hashtable)graph[node.val];

            if (node.left != null)
            {
                if (!children.ContainsKey(node.left.val)) children.Add(node.left.val, true);
                if (!graph.ContainsKey(node.left.val)) graph.Add(node.left.val, new Hashtable());
                Hashtable leftChildren = (Hashtable)graph[node.left.val];
                if (!leftChildren.ContainsKey(node.val)) leftChildren.Add(node.val, true);
                queue.Enqueue(node.left);
            }
            if (node.right != null)
            {
                if (!children.ContainsKey(node.right.val)) children.Add(node.right.val, true);
                if (!graph.ContainsKey(node.right.val)) graph.Add(node.right.val, new Hashtable());
                Hashtable rightChildren = (Hashtable)graph[node.right.val];
                if (!rightChildren.ContainsKey(node.val)) rightChildren.Add(node.val, true);
                queue.Enqueue(node.right);
            }
        }

        Hashtable visitedNode = new Hashtable();
        visitedNode.Add(start, true);
        int retVal = 0;
        FindLongestPath(graph, start, visitedNode, 0, ref retVal);
        return retVal;
    }

    private void FindLongestPath(Hashtable graph,
                                 int node,
                                 Hashtable visitedNode,
                                 int currentPathLen,
                                 ref int longestPathLen)
    {
        if (!graph.ContainsKey(node)) return;

        longestPathLen = Math.Max(longestPathLen, currentPathLen);
        Hashtable children = (Hashtable)graph[node];
        foreach (int child in children.Keys)
        {
            if (!visitedNode.ContainsKey(child))
            {
                visitedNode.Add(child, true);
                FindLongestPath(graph, child, visitedNode, currentPathLen + 1, ref longestPathLen);
            }
        }
    }
}