Palindrome With Errors - Part 2
Hello folks,
back from a trip to Europe, and with a nasty flu virus type A. In any case, I realized that I never posted the follow-up to the "palindrome with errors" problem - so here it is.
As I had mentioned, a naïve brute-force solution would lead to a runtime of O(2^(length of string)), which given the constraints of length of string <= 120,000, such solution would be intractable.
A slightly better solution is still exponential, but exponential in the max number of errors which the problem limits to 13. The solution below will work in O(3^13), or ~2,000,000 steps, which is super fast.
The idea is to analyze the string as if it was already a palindrome. Therefore, take a look at the extremes of the string. If they match, then it is so far a palindrome. In which case you continue the analysis by moving inwards.
The moment that you determine that the extremes don't match, that's when the exponential aspect will take place. What you'd have to do then is recursively try the following:
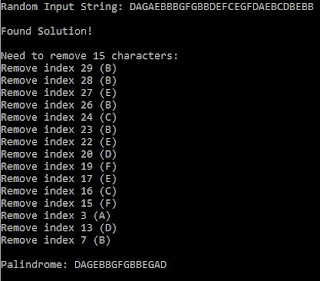
Notice that the bad side effect of this solution is that if the max number of errors allowed is a huge number, it will be intractable. But given the constraints in the original problem, it should work. As an example, here is a run when the max number of errors allowed was set to 15:
back from a trip to Europe, and with a nasty flu virus type A. In any case, I realized that I never posted the follow-up to the "palindrome with errors" problem - so here it is.
As I had mentioned, a naïve brute-force solution would lead to a runtime of O(2^(length of string)), which given the constraints of length of string <= 120,000, such solution would be intractable.
A slightly better solution is still exponential, but exponential in the max number of errors which the problem limits to 13. The solution below will work in O(3^13), or ~2,000,000 steps, which is super fast.
The idea is to analyze the string as if it was already a palindrome. Therefore, take a look at the extremes of the string. If they match, then it is so far a palindrome. In which case you continue the analysis by moving inwards.
The moment that you determine that the extremes don't match, that's when the exponential aspect will take place. What you'd have to do then is recursively try the following:
- Assume that you remove the leftmost character, and try again
- Assume that you remove the rightmost character, and try again
- Assume that you remove both the leftmost and the rightmost characters, and try again
Notice that the bad side effect of this solution is that if the max number of errors allowed is a huge number, it will be intractable. But given the constraints in the original problem, it should work. As an example, here is a run when the max number of errors allowed was set to 15:
Code is down below, thanks, Marcelo.
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace PalindromeWithErrorsEx
{
class Program
{
static void Main(string[] args)
{
if (args.Length != 2)
{
Console.WriteLine("Usage: PalindromeWithErrorsEx.exe <max number of errors> <random string length>");
return;
}
{
class Program
{
static void Main(string[] args)
{
if (args.Length != 2)
{
Console.WriteLine("Usage: PalindromeWithErrorsEx.exe <max number of errors> <random string length>");
return;
}
int maxNumberOfErrorsAllowed = Convert.ToInt32(args[0]);
int stringLen = Convert.ToInt32(args[1]);
int stringLen = Convert.ToInt32(args[1]);
string str = GenerateRandomString(stringLen);
Console.WriteLine("Random Input String: {0}", str);
Console.WriteLine();
HashSet<int> indexesToBeRemoved = new HashSet<int>();
Console.WriteLine("Random Input String: {0}", str);
Console.WriteLine();
HashSet<int> indexesToBeRemoved = new HashSet<int>();
if (RemoveErrorsToGeneratePalindrome(str,
0,
str.Length - 1,
maxNumberOfErrorsAllowed,
0,
indexesToBeRemoved))
{
Console.WriteLine("Found Solution!");
Console.WriteLine();
0,
str.Length - 1,
maxNumberOfErrorsAllowed,
0,
indexesToBeRemoved))
{
Console.WriteLine("Found Solution!");
Console.WriteLine();
Console.WriteLine("Need to remove {0} characters:", indexesToBeRemoved.Count);
foreach (int i in indexesToBeRemoved)
{
Console.WriteLine("Remove index {0} ({1})", i, str[i]);
}
Console.WriteLine();
foreach (int i in indexesToBeRemoved)
{
Console.WriteLine("Remove index {0} ({1})", i, str[i]);
}
Console.WriteLine();
string palindromeStr = "";
for (int i = 0; i < str.Length; i++)
{
if (!indexesToBeRemoved.Contains(i))
{
palindromeStr += str[i].ToString();
}
}
Console.WriteLine("Palindrome: {0}", palindromeStr);
}
else
{
Console.WriteLine("Solution Not Found!");
}
}
for (int i = 0; i < str.Length; i++)
{
if (!indexesToBeRemoved.Contains(i))
{
palindromeStr += str[i].ToString();
}
}
Console.WriteLine("Palindrome: {0}", palindromeStr);
}
else
{
Console.WriteLine("Solution Not Found!");
}
}
static string GenerateRandomString(int len)
{
string chars = "abcdefg".ToUpper();
Random rd = new Random();
{
string chars = "abcdefg".ToUpper();
Random rd = new Random();
string str = "";
for (int i = 0; i < len; i++)
{
str += chars[rd.Next(0, chars.Length)].ToString();
}
for (int i = 0; i < len; i++)
{
str += chars[rd.Next(0, chars.Length)].ToString();
}
return str;
}
}
static bool RemoveErrorsToGeneratePalindrome(string str,
int beginIndex,
int endIndex,
int maxNumberErrorsAllowed,
int currentNumberErrors,
HashSet<int> indexesToBeRemoved)
{
if (currentNumberErrors > maxNumberErrorsAllowed)
{
return false;
}
if (beginIndex >= endIndex)
{
return true;
}
int beginIndex,
int endIndex,
int maxNumberErrorsAllowed,
int currentNumberErrors,
HashSet<int> indexesToBeRemoved)
{
if (currentNumberErrors > maxNumberErrorsAllowed)
{
return false;
}
if (beginIndex >= endIndex)
{
return true;
}
if (str[beginIndex] == str[endIndex])
{
return RemoveErrorsToGeneratePalindrome(str,
beginIndex + 1,
endIndex - 1,
maxNumberErrorsAllowed,
currentNumberErrors,
indexesToBeRemoved);
}
else
{
//Attempt to remove the last index
if (!indexesToBeRemoved.Contains(endIndex))
{
indexesToBeRemoved.Add(endIndex);
}
{
return RemoveErrorsToGeneratePalindrome(str,
beginIndex + 1,
endIndex - 1,
maxNumberErrorsAllowed,
currentNumberErrors,
indexesToBeRemoved);
}
else
{
//Attempt to remove the last index
if (!indexesToBeRemoved.Contains(endIndex))
{
indexesToBeRemoved.Add(endIndex);
}
if (RemoveErrorsToGeneratePalindrome(str,
beginIndex,
endIndex - 1,
maxNumberErrorsAllowed,
currentNumberErrors + 1,
indexesToBeRemoved))
{
return true;
}
beginIndex,
endIndex - 1,
maxNumberErrorsAllowed,
currentNumberErrors + 1,
indexesToBeRemoved))
{
return true;
}
if (indexesToBeRemoved.Contains(endIndex))
{
indexesToBeRemoved.Remove(endIndex);
}
{
indexesToBeRemoved.Remove(endIndex);
}
//Attempt to remove the first index
if (!indexesToBeRemoved.Contains(beginIndex))
{
indexesToBeRemoved.Add(beginIndex);
}
if (!indexesToBeRemoved.Contains(beginIndex))
{
indexesToBeRemoved.Add(beginIndex);
}
if (RemoveErrorsToGeneratePalindrome(str,
beginIndex + 1,
endIndex,
maxNumberErrorsAllowed,
currentNumberErrors + 1,
indexesToBeRemoved))
{
return true;
}
beginIndex + 1,
endIndex,
maxNumberErrorsAllowed,
currentNumberErrors + 1,
indexesToBeRemoved))
{
return true;
}
if (indexesToBeRemoved.Contains(beginIndex))
{
indexesToBeRemoved.Remove(beginIndex);
}
{
indexesToBeRemoved.Remove(beginIndex);
}
//Attempt to remove both the first and the last indexes
if (!indexesToBeRemoved.Contains(beginIndex))
{
indexesToBeRemoved.Add(beginIndex);
}
if (!indexesToBeRemoved.Contains(endIndex))
{
indexesToBeRemoved.Add(endIndex);
}
if (!indexesToBeRemoved.Contains(beginIndex))
{
indexesToBeRemoved.Add(beginIndex);
}
if (!indexesToBeRemoved.Contains(endIndex))
{
indexesToBeRemoved.Add(endIndex);
}
if (RemoveErrorsToGeneratePalindrome(str,
beginIndex + 1,
endIndex - 1,
maxNumberErrorsAllowed,
currentNumberErrors + 2,
indexesToBeRemoved))
{
return true;
}
beginIndex + 1,
endIndex - 1,
maxNumberErrorsAllowed,
currentNumberErrors + 2,
indexesToBeRemoved))
{
return true;
}
if (indexesToBeRemoved.Contains(endIndex))
{
indexesToBeRemoved.Remove(endIndex);
}
if (indexesToBeRemoved.Contains(beginIndex))
{
indexesToBeRemoved.Remove(beginIndex);
}
}
{
indexesToBeRemoved.Remove(endIndex);
}
if (indexesToBeRemoved.Contains(beginIndex))
{
indexesToBeRemoved.Remove(beginIndex);
}
}
return false;
}
}
}
}
}
}



As correctly pointed out by a friend, Fred Cruz, no connection with Ted Cruz, and arguably one of the top 10 developers alive, the execution time can be reduced to 2^(number of errors) by removing the redundant last recursive call, hence removing this code:
ReplyDelete//Attempt to remove both the first and the last indexes
if (!indexesToBeRemoved.Contains(beginIndex))
{
indexesToBeRemoved.Add(beginIndex);
}
if (!indexesToBeRemoved.Contains(endIndex))
{
indexesToBeRemoved.Add(endIndex);
}
if (RemoveErrorsToGeneratePalindrome(str,
beginIndex + 1,
endIndex - 1,
maxNumberErrorsAllowed,
currentNumberErrors + 2,
indexesToBeRemoved))
{
return true;
}
if (indexesToBeRemoved.Contains(endIndex))
{
indexesToBeRemoved.Remove(endIndex);
}
if (indexesToBeRemoved.Contains(beginIndex))
{
indexesToBeRemoved.Remove(beginIndex);
}
Thanks for sharing an interesting problem Marcelo! My gut feeling and overlapping recursive calls make me wonder if this problem cannot be solved by using dynamic programming, where the state is defined as D[i,j] - the minimum number of errors required to turn S[i:j] into palindrome. So D[i,j] = D[i+1,j-1] if S[i] == S[j] and min(D[i+1,j], D[i,j-1]) otherwise. I'm too lazy to think about bottom up solution, but using memoization this should be fairly simple to implement and have O(N^2) time and space complexity, since we basically need to populate half of the N*N matrix (i <= j). Oh, and end result would be determined by D[0,n-1] <= maxNumberErrorsAllowed.
ReplyDeleteGet well soon!
Being as absentminded as usually I forgot to add "+ 1" to D[i,j] state definition when S[i] != S[j], so the formula should be "min(D[i+1,j], D[i,j-1]) + 1". Hopefully I'll have a chance to try this algorithm in action soon...
ReplyDeleteCool, I had 5 minutes to spare, so here is my take on this problem - http://ideone.com/LEe73A
ReplyDeleteimport functools
S = input()
max_errors_allowed = int(input())
def is_almost_palindrome(text, max_errors_allowed):
@functools.lru_cache(maxsize=None)
def get_state(i, j):
if i >= j:
return 0
if text[i] == text[j]:
return get_state(i+1, j-1)
return min(get_state(i+1, j), get_state(i,j-1)) + 1
return get_state(0, len(text)-1) <= max_errors_allowed
print(is_almost_palindrome(S, max_errors_allowed))
As it stands right now the implementation does not print removed indices, but it's straightforward it to use an array of "parents" to record states from which we got to a "child" state and iterate over "parents" array to trace the path to D[0,n-1]
I just realized that the matrix size to store the state would be ~13GB or ~7GB (assuming min errors required can fit into a single byte, which is not necessarily true) if we use sparse representation, since we just need half of it, so the simple python script I wrote won't quite work for strings with 120000 characters, but it's still doable using explicit arrays in more memory conservative language like C++ and enough of RAM :)
ReplyDeleteWhile thinking about this, I also realized that your implementation can potentially have really deep invocation tree, which would almost certainly result in StackOverflowException :)
Awesome insight, Taras! You reduced the problem quite elegantly to DP (which has never been my stronghold...). The GBs of mem will be a concern indeed. I did not come across an overflow error given the constraints of the input and that the (modified) algorithm runs in 2^K time with K<=13. Thanks again for collaborating!
ReplyDeleteDP is magic and for the most part just an optimization, whereas your solution is very easy to understand and reason about. I always prefer to start simple to get a better understanding of the problem and its properties and optimize only if necessary. Also I agree that for given constraints StackOverflowException is unlikely to be an issue, though for large enough K it will.
DeleteAnyways, thanks again for an excellent problem and an excellent solution!