Ugly Number 2: a tale of an inefficient solution that does the job
Problem is posted here: https://leetcode.com/problems/ugly-number-ii/, or copied/pasted:
The limits are small enough (N<=1690) that I thought a not fancy solution (meaning not Dynamic Programming one) could do the trick. The solution will run in O(NLogN)-time:
a) First we'll use a heap based on a priority queue implementation to store all the numbers from the 1st to the Nth (the solution). It will clearly consume some good amount of extra memory.
b) At the same time we use hash table to mark the numbers seen before and already added to the heap
c) We'll iterate from 1..N (hence the "N" in the Big-O time complexity). For each element retrieve from the heal (hence the "LogN"). Add back the ones that we have not seen (not in the hash table) by multiplying the current number to the given primes (2,3,5).
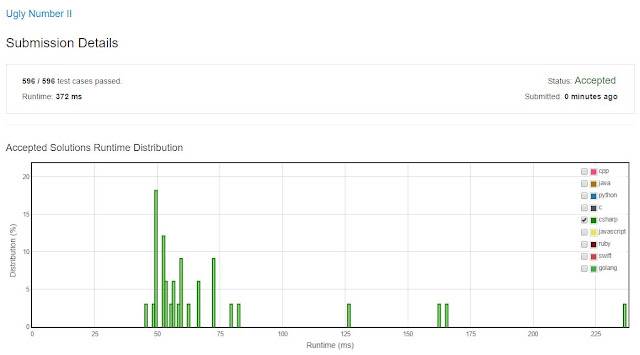
The solution takes a relatively long time and it is off the chart as you can see below - but did the job, it was accepted. Some times in life all you want is to be accepted, even if you barely make the list :). Love, Marcelo (code below).
using System;
using System.Collections;
using System.Collections.Generic;
using System.Linq;
using System.Numerics;
using System.Text;
using System.Threading.Tasks;
using System.IO;
namespace LeetCode
{
class Program
{
static void Main(string[] args)
{
Solution sol = new Solution();
Console.WriteLine(sol.NthUglyNumber(Convert.ToInt32(args[0])));
}
}
public class Solution
{
public int NthUglyNumber(int n)
{
/*
* Approach:
* 1) keep a hash table of the numbers visited
* 2) use a heap (priority queue) to get the next ith number
* 3) iterate adding back new numbers to the priority queue until you find the nth
*/
Hashtable htVisited = new Hashtable();
PriorityQueue pq = new PriorityQueue(3 * 1690, false);
pq.Enqueue(1L, 1L);
htVisited.Add(1L, true);
long candidate = 1;
long[] primes = { 2, 3, 5 };
while (n > 0)
{
candidate = (long)pq.Dequeue();
for (int i = 0; i < primes.Length; i++)
{
long next = candidate * primes[i];
if(!htVisited.ContainsKey(next))
{
htVisited.Add(next, true);
pq.Enqueue(next, next);
}
}
n--;
}
return (int)candidate;
}
}
/*By-the-book PriorityQueue*/
public class PriorityQueue
{
public struct HeapEntry
{
private object item;
private long priority;
public HeapEntry(object item, long priority)
{
this.item = item;
this.priority = priority;
}
public object Item
{
get
{
return item;
}
}
public long Priority
{
get
{
return priority;
}
}
}
private long count;
private long capacity;
private bool descending; //Means that the max element at the top
private HeapEntry[] heap;
public long Count
{
get
{
return this.count;
}
}
public PriorityQueue(long capacity, bool descending)
{
this.capacity = capacity;
this.descending = descending;
heap = new HeapEntry[this.capacity];
}
public object Dequeue()
{
object result = heap[0].Item;
count--;
trickleDown(0, heap[count]);
return result;
}
public void Enqueue(object item, long priority)
{
count++;
bubbleUp(count - 1, new HeapEntry(item, priority));
}
private void bubbleUp(long index, HeapEntry he)
{
long parent = (index - 1) / 2;
// note: (index > 0) means there is a parent
while (
(index > 0) &&
((this.descending && heap[parent].Priority < he.Priority) || (!this.descending && heap[parent].Priority > he.Priority))
)
{
heap[index] = heap[parent];
index = parent;
parent = (index - 1) / 2;
}
heap[index] = he;
}
private void trickleDown(long index, HeapEntry he)
{
long child = (index * 2) + 1;
while (child < count)
{
if (
((child + 1) < count) &&
((this.descending && heap[child].Priority < heap[child + 1].Priority) || (!this.descending && heap[child].Priority > heap[child + 1].Priority))
)
{
child++;
}
heap[index] = heap[child];
index = child;
child = (index * 2) + 1;
}
bubbleUp(index, he);
}
}
}
Write a program to find then-th ugly number.Ugly numbers are positive numbers whose prime factors only include2, 3, 5. For example,1, 2, 3, 4, 5, 6, 8, 9, 10, 12is the sequence of the first10ugly numbers.Note that1is typically treated as an ugly number, and n does not exceed 1690.
The limits are small enough (N<=1690) that I thought a not fancy solution (meaning not Dynamic Programming one) could do the trick. The solution will run in O(NLogN)-time:
a) First we'll use a heap based on a priority queue implementation to store all the numbers from the 1st to the Nth (the solution). It will clearly consume some good amount of extra memory.
b) At the same time we use hash table to mark the numbers seen before and already added to the heap
c) We'll iterate from 1..N (hence the "N" in the Big-O time complexity). For each element retrieve from the heal (hence the "LogN"). Add back the ones that we have not seen (not in the hash table) by multiplying the current number to the given primes (2,3,5).
The solution takes a relatively long time and it is off the chart as you can see below - but did the job, it was accepted. Some times in life all you want is to be accepted, even if you barely make the list :). Love, Marcelo (code below).
using System.Collections;
using System.Collections.Generic;
using System.Linq;
using System.Numerics;
using System.Text;
using System.Threading.Tasks;
using System.IO;
namespace LeetCode
{
class Program
{
static void Main(string[] args)
{
Solution sol = new Solution();
Console.WriteLine(sol.NthUglyNumber(Convert.ToInt32(args[0])));
}
}
public class Solution
{
public int NthUglyNumber(int n)
{
/*
* Approach:
* 1) keep a hash table of the numbers visited
* 2) use a heap (priority queue) to get the next ith number
* 3) iterate adding back new numbers to the priority queue until you find the nth
*/
Hashtable htVisited = new Hashtable();
PriorityQueue pq = new PriorityQueue(3 * 1690, false);
pq.Enqueue(1L, 1L);
htVisited.Add(1L, true);
long candidate = 1;
long[] primes = { 2, 3, 5 };
while (n > 0)
{
candidate = (long)pq.Dequeue();
for (int i = 0; i < primes.Length; i++)
{
long next = candidate * primes[i];
if(!htVisited.ContainsKey(next))
{
htVisited.Add(next, true);
pq.Enqueue(next, next);
}
}
n--;
}
return (int)candidate;
}
}
/*By-the-book PriorityQueue*/
public class PriorityQueue
{
public struct HeapEntry
{
private object item;
private long priority;
public HeapEntry(object item, long priority)
{
this.item = item;
this.priority = priority;
}
public object Item
{
get
{
return item;
}
}
public long Priority
{
get
{
return priority;
}
}
}
private long count;
private long capacity;
private bool descending; //Means that the max element at the top
private HeapEntry[] heap;
public long Count
{
get
{
return this.count;
}
}
public PriorityQueue(long capacity, bool descending)
{
this.capacity = capacity;
this.descending = descending;
heap = new HeapEntry[this.capacity];
}
public object Dequeue()
{
object result = heap[0].Item;
count--;
trickleDown(0, heap[count]);
return result;
}
public void Enqueue(object item, long priority)
{
count++;
bubbleUp(count - 1, new HeapEntry(item, priority));
}
private void bubbleUp(long index, HeapEntry he)
{
long parent = (index - 1) / 2;
// note: (index > 0) means there is a parent
while (
(index > 0) &&
((this.descending && heap[parent].Priority < he.Priority) || (!this.descending && heap[parent].Priority > he.Priority))
)
{
heap[index] = heap[parent];
index = parent;
parent = (index - 1) / 2;
}
heap[index] = he;
}
private void trickleDown(long index, HeapEntry he)
{
long child = (index * 2) + 1;
while (child < count)
{
if (
((child + 1) < count) &&
((this.descending && heap[child].Priority < heap[child + 1].Priority) || (!this.descending && heap[child].Priority > heap[child + 1].Priority))
)
{
child++;
}
heap[index] = heap[child];
index = child;
child = (index * 2) + 1;
}
bubbleUp(index, he);
}
}
}



Very nice! As you've mentioned, this problem can be solved differently, for example by looking at the pattern of how powers of prime numbers increase with every next ugly number, it's not too hard to devise a strategy of generating next prime factor powers, but my initial attempt to solve this problem was pretty much identical to yours, because it's easy, fast enough and very generic. This method can be used to generate all sorts of sequences and is applicable to many problems.
ReplyDeleteSince C++ has a built-in priority queue implementation C++'s solution using the same approach is a bit shorter though :)
class Solution {
public:
int nthUglyNumber(int n) {
array primes = {2, 3, 5};
unordered_set visited {1};
priority_queue, greater> frontier;
frontier.push(1);
long ugly;
for (int count = 0; count < n; ++count) {
ugly = frontier.top(); frontier.pop();
for (int prime : primes) {
long next = ugly * prime;
if (!visited.insert(next).second) continue; // already visited
frontier.push(next);
}
}
return ugly;
}
};
Thanks for sharing this problem!
Built-in priority queue: cool!!! Wondering if .net has one too?
ReplyDeletelooks like it does not :( You should consider switching to Java, since it has PriorityQueue and many other useful algorithms ;)
Delete