Queens That Can Attack the King: Modularization

Problem is here: https://leetcode.com/problems/queens-that-can-attack-the-king/

On an 8x8 chessboard, there can be multiple Black Queens and one White King.

Given an array of integer coordinates queens that represents the positions of the Black Queens, and a pair of coordinates king that represent the position of the White King, return the coordinates of all the queens (in any order) that can attack the King.

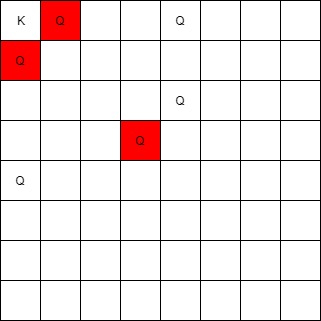
Example 1:

Input: queens = [[0,1],[1,0],[4,0],[0,4],[3,3],[2,4]], king = [0,0]
Output: [[0,1],[1,0],[3,3]]
Explanation:  
The queen at [0,1] can attack the king cause they're in the same row. 
The queen at [1,0] can attack the king cause they're in the same column. 
The queen at [3,3] can attack the king cause they're in the same diagnal. 
The queen at [0,4] can't attack the king cause it's blocked by the queen at [0,1]. 
The queen at [4,0] can't attack the king cause it's blocked by the queen at [1,0]. 
The queen at [2,4] can't attack the king cause it's not in the same row/column/diagnal as the king.

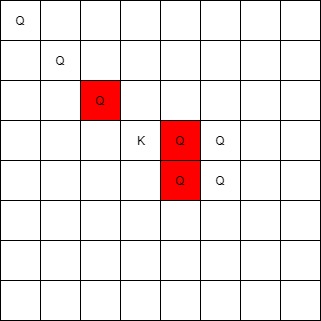
Example 2:

Input: queens = [[0,0],[1,1],[2,2],[3,4],[3,5],[4,4],[4,5]], king = [3,3]
Output: [[2,2],[3,4],[4,4]]

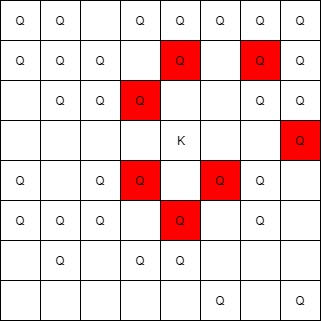
Example 3:

Input: queens = [[5,6],[7,7],[2,1],[0,7],[1,6],[5,1],[3,7],[0,3],[4,0],[1,2],[6,3],[5,0],[0,4],[2,2],[1,1],[6,4],[5,4],[0,0],[2,6],[4,5],[5,2],[1,4],[7,5],[2,3],[0,5],[4,2],[1,0],[2,7],[0,1],[4,6],[6,1],[0,6],[4,3],[1,7]], king = [3,4]
Output: [[2,3],[1,4],[1,6],[3,7],[4,3],[5,4],[4,5]]

Constraints:

• 1 <= queens.length <= 63
• queens[0].length == 2
• 0 <= queens[i][j] < 8
• king.length == 2
• 0 <= king[0], king[1] < 8
• At most one piece is allowed in a cell.

Modularize the solution so that you can test all the 8 directions in an easy and bugs-free manner. Once you have one small function that does all that you need, the code becomes very simple. Below - cheer, ACC.

public class Solution
{
    public IList<IList<int>> QueensAttacktheKing(int[][] queens, int[] king)
    {
        Hashtable queensPlace = new Hashtable();
        for (int i = 0; i < queens.GetLength(0); i++)
        {
            int key = queens[i][0] * 100 + queens[i][1];
            if (!queensPlace.ContainsKey(key)) queensPlace.Add(key, true);
        }

        List<IList<int>> retVal = new List<IList<int>>();
        for (int i = 0; i < queens.GetLength(0); i++)
        {
            bool north = true;
            bool south = true;
            bool east = true;
            bool west = true;
            bool ne = true;
            bool nw = true;
            bool se = true;
            bool sw = true;

            for (int j = 1; j <= 10; j++)
            {
                if (!north &&
                    !south &&
                    !east &&
                    !west &&
                    !ne &&
                    !nw &&
                    !se &&
                    !sw) break;

                //North
                CheckPosition(queensPlace, queens[i][0], queens[i][1], queens[i][0] - j, queens[i][1], king, retVal, ref north);
                //South
                CheckPosition(queensPlace, queens[i][0], queens[i][1], queens[i][0] + j, queens[i][1], king, retVal, ref south);
                //East
                CheckPosition(queensPlace, queens[i][0], queens[i][1], queens[i][0], queens[i][1] + j, king, retVal, ref east);
                //West
                CheckPosition(queensPlace, queens[i][0], queens[i][1], queens[i][0], queens[i][1] - j, king, retVal, ref west);
                //Northeast
                CheckPosition(queensPlace, queens[i][0], queens[i][1], queens[i][0] - j, queens[i][1] + j, king, retVal, ref ne);
                //Southeast
                CheckPosition(queensPlace, queens[i][0], queens[i][1], queens[i][0] + j, queens[i][1] + j, king, retVal, ref se);
                //Northwest
                CheckPosition(queensPlace, queens[i][0], queens[i][1], queens[i][0] - j, queens[i][1] - j, king, retVal, ref nw);
                //Southwest
                CheckPosition(queensPlace, queens[i][0], queens[i][1], queens[i][0] + j, queens[i][1] - j, king, retVal, ref sw);
            }
        }

        return retVal;
    }

    private void CheckPosition(Hashtable queensPlace,
                                int originalQueenRow,
                                int originalQueenCol,
                                int row,
                                int col,
                                int[] king,
                                List<IList<int>> retVal,
                                ref bool direction)
    {
        if (!direction) return;
        if (row < 0 || row >= 8 || col < 0 || col >= 8)
        {
            direction = false;
            return;
        }
        int key = row * 100 + col;
        if (queensPlace.ContainsKey(key))
        {
            direction = false;
            return;
        }
        if (king[0] == row && king[1] == col)
        {
            retVal.Add(new List<int> { originalQueenRow, originalQueenCol });
            direction = false;
        }
    }
}