Finding the Diameter of an N-Ary Tree: the "To-And-Thru" approach

-
Hello folks, this is a problem that exemplifies a technique that I like to call the To-And-Thru. We want to find the diameter of an N-ary tree (meaning a tree where each node has 0, 1 or more children). Take a look: https://leetcode.com/problems/diameter-of-n-ary-tree/

What you want is a near-linear solution in the number of nodes. If you assume that the tree has N nodes, and that each node has an average of LogN children, then the To-And-Thru algorithm below will run in O(N * (LogN)^2) time. Not really linear, but something that seems to be closer to NLogN.

The idea is the following:
  1. Post-Order DFS
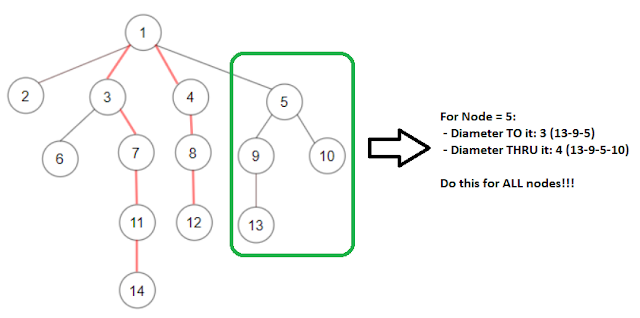
  2. For each node, compute the following:
    1. The longest path TO the node
    2. The longest path THRU the node
  3. The above computation will take LogN*LogN since there are two nested loops (I guess there might be a way to reduce this to LogN, meaning one loop)
  4. As you compute 2.1 and 2.2, your diameter will be the Max
See figure below. Works well enough. Code is down below, stay safe, stay motivated!!! ACC



public class Solution {
    public int Diameter(Node root)
    {
        int maxThruNode = 0;
        int maxToNode = 0;
        int diameter = 0;

        Diameter(root, ref maxThruNode, ref maxToNode, ref diameter);

        return diameter > 0 ? diameter - 1 : diameter; //I'm counting the number of nodes in the path. Number of edges is #nodes-1
    }

    private void Diameter(Node node,
                          ref int maxThruNode,
                          ref int maxToNode,
                          ref int diameter)
    {
        if (node == null) return;

        if (node.children.Count == 0)
        {
            maxThruNode = 1;
            maxToNode = 1;
            return;
        }

        int[] childMaxThruNode = new int[node.children.Count];
        int[] childMaxToNode = new int[node.children.Count];

        int index = 0;
        foreach (Node child in node.children)
        {
            Diameter(child, ref childMaxThruNode[index], ref childMaxToNode[index], ref diameter);
            index++;
        }

        maxThruNode = 0;
        maxToNode = 0;
        for (int i = 0; i < childMaxThruNode.Length; i++)
        {
            maxToNode = Math.Max(childMaxToNode[i] + 1, maxToNode);
            diameter = Math.Max(maxToNode, diameter);
            for (int j = i + 1; j < childMaxThruNode.Length; j++)
            {
                maxThruNode = Math.Max(childMaxToNode[i] + childMaxToNode[j] + 1, maxThruNode);
                maxToNode = Math.Max(childMaxToNode[i] + 1, maxToNode);
                maxToNode = Math.Max(childMaxToNode[j] + 1, maxToNode);
                diameter = Math.Max(maxThruNode, diameter);
                diameter = Math.Max(maxToNode, diameter);
            }
        }
    }
}

Comments

Post a Comment

Popular posts from this blog

Advent of Code - Day 6, 2024: BFS and FSM

-
Image
To solve this Advent of Code (parts 1 and 2), I used Breadth-First Search (BFS) to keep moving the guard as well as Finite State Machine (FSM) to control the directions. This solves part 1 easily. Part 2 can be solved using the same technique, takes a little longer since you need to try every empty cell, but it eventually does the trick (takes a min or so). Code is down below, cheers, ACC. Day 6 - Advent of Code 2024 using System.IO; using System.Collections; using System; using System.Text; using System.Text.RegularExpressions; using System.ComponentModel.DataAnnotations; Process2(); void Process() { string fileName = "input.txt"; FileInfo fileInfo = new FileInfo(fileName); StreamReader sr = fileInfo.OpenText(); List map = new List (); int startRow = 0; int startCol = 0; while (!sr.EndOfStream) { string line = sr.ReadLine().Trim(); map.Add(new StringBuilder(line)); int indexStart = line.IndexOf('^'); ...
Read more

Golang vs. C#: performance characteristics (simple case study)

-
Image
This is an interesting example to study the performance characteristics of Golang compared to C# for a very particular case (not generalized though).  The same code was written in C# and Golang (literally translated from one to the other). Below you'll be able to see the source code for both. The problem is a simple post-order DFS in a tree-like graph. The code in C# times out (TLE = Time Limited Exceeded). The code in Golang not only works but beats 100% of the other Golang submissions. Take a look the image below: Some potential reasons for the performance gains from Go in this particular example are: 1. Language and Runtime Differences:    Go is compiled directly to machine code, while C# typically runs on a virtual machine (CLR).    Go has a simpler runtime with less overhead compared to the .NET runtime.    Go's garbage collector is designed for low latency, which can lead to better performance in some scenarios. 2. Data Structures:    G...
Read more

Advent of Code - Day 7, 2024: Backtracking and Eval

-
Image
Problem today requires backtracking and eval (evaluating a mathematical expression in the format of a string). Glad that it used a left-2-right evaluation, makes for an easy parsing and not overly complicated evaluation function. Code is down below for parts 1 and 2. Cheers, ACC. Day 7 - Advent of Code 2024 using System.IO; using System.Collections; using System; using System.Text; using System.Text.RegularExpressions; using System.ComponentModel.DataAnnotations; Process2(); void Process() { string fileName = "input.txt"; long retVal = 0; FileInfo fileInfo = new FileInfo(fileName); StreamReader sr = fileInfo.OpenText(); while (!sr.EndOfStream) { string line = sr.ReadLine().Trim(); string[] parts1 = line.Split(':'); long target = Int64.Parse(parts1[0]); string[] numbers = parts1[1].Split(new char[] { ' ' }, StringSplitOptions.RemoveEmptyEntries); if (TryAll1(numbers, target, "", 0)) r...
Read more