Friday Night Dijkstra's Algorithm

Covid-times Friday Night - Dijkstra's Algorithm. 

Check out this problem: https://leetcode.com/problems/path-with-minimum-effort/

You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where heights[row][col] represents the height of cell (row, col). You are situated in the top-left cell, (0, 0), and you hope to travel to the bottom-right cell, (rows-1, columns-1) (i.e., 0-indexed). You can move up, down, left, or right, and you wish to find a route that requires the minimum effort.

A route's effort is the maximum absolute difference in heights between two consecutive cells of the route.

Return the minimum effort required to travel from the top-left cell to the bottom-right cell.

 

Example 1:

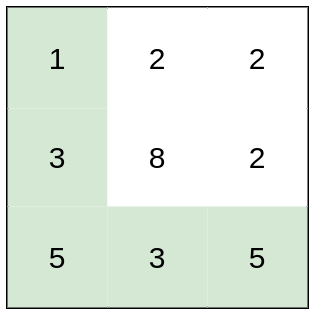
Input: heights = [[1,2,2],[3,8,2],[5,3,5]]
Output: 2
Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.

Example 2:

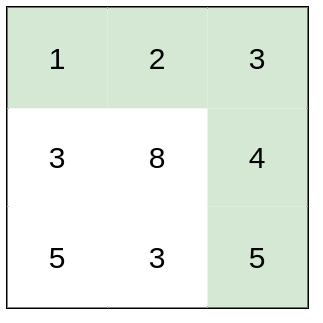
Input: heights = [[1,2,3],[3,8,4],[5,3,5]]
Output: 1
Explanation: The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5].

Example 3:

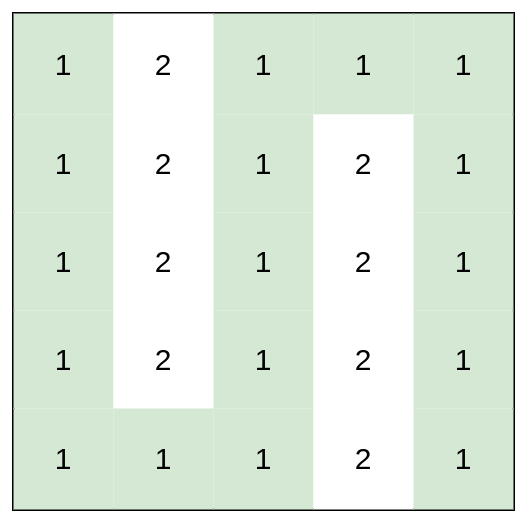
Input: heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
Output: 0
Explanation: This route does not require any effort.

 

Constraints:

• rows == heights.length
• columns == heights[i].length
• 1 <= rows, columns <= 100
• 1 <= heights[i][j] <= 106

Accepted

6,380

Submissions

16,528

My first attempt was DP, which works if-and-only-if the matrix traversal is down or right, but since it allows all four directions, then DP won't cut it. Better is to apply Dijkstra's Algorithm:

1. Requires a Priority Queue (I always keep one implementation handy)
2. Requires a hash map/table to mark visits
3. Use a smart unique key (rows * (LEN+1) + col)
4. Each queue item contains the row, the col, the unique key, and the max effort so far
5. The priority queue is weighted by min effort
6. Main aspect with Dijkstra's is to only mark as visited after the dequeue. Don't mark as visited during the enqueue. Allow for enqueuing the same cell (with different efforts) multiple times

Code is down below. Have a great night everyone, stay safe, and vote!!! ACC

public class QueueItem
{
    public int row = 0;
    public int col = 0;
    public int effort = 0;
    public int key = 0;
    public QueueItem(int row, int col, int effort)
    {
        this.row = row;
        this.col = col;
        this.effort = effort;
        this.key = row * 200 + col;
    }
}
public class Solution
{
    public int MinimumEffortPath(int[][] heights)
    {
        Hashtable visited = new Hashtable();
        PriorityQueue pqueue = new PriorityQueue();

        QueueItem qi = new QueueItem(0, 0, 0);
        visited.Add(qi.key, true);
        pqueue.Enqueue(qi, qi.effort);

        while (pqueue.Count > 0)
        {
            QueueItem current = (QueueItem)pqueue.Dequeue();
            if (!visited.ContainsKey(current.key)) visited.Add(current.key, true);

            if (current.row == heights.Length - 1 && current.col == heights[0].Length - 1) return current.effort;

            int[] dr = { -1, 1, 0, 0 };
            int[] dc = { 0, 0, 1, -1 };

            for (int i = 0; i < dr.Length; i++)
            {
                int row = current.row + dr[i];
                int col = current.col + dc[i];

                if (row >= 0 &&
                    row < heights.Length &&
                    col >= 0 &&
                    col < heights[0].Length)
                {
                    QueueItem nqi = new QueueItem(row, col, Math.Max(current.effort, Math.Abs(heights[row][col] - heights[current.row][current.col])));
                    if (!visited.ContainsKey(nqi.key))
                    {
                        pqueue.Enqueue(nqi, nqi.effort);
                    }
                }
            }
        }

        return 0;
    }
}

public class PriorityQueue
{
    public struct HeapEntry
    {
        private object item;
        private double priority;
        public HeapEntry(object item, double priority)
        {
            this.item = item;
            this.priority = priority;
        }
        public object Item
        {
            get
            {
                return item;
            }
        }
        public double Priority
        {
            get
            {
                return priority;
            }
        }
    }

    private int count;
    private int capacity;
    private HeapEntry[] heap;

    public int Count
    {
        get
        {
            return this.count;
        }
    }

    public PriorityQueue()
    {
        capacity = 1000000;
        heap = new HeapEntry[capacity];
    }

    public object Dequeue(/*out double priority*/)
    {
        //priority = heap[0].Priority;
        object result = heap[0].Item;
        count--;
        trickleDown(0, heap[count]);
        return result;
    }

    public void Enqueue(object item, double priority)
    {
        count++;
        bubbleUp(count - 1, new HeapEntry(item, priority));
    }

    private void bubbleUp(int index, HeapEntry he)
    {
        int parent = (index - 1) / 2;
        // note: (index > 0) means there is a parent
        while ((index > 0) && (heap[parent].Priority > he.Priority))
        {
            heap[index] = heap[parent];
            index = parent;
            parent = (index - 1) / 2;
        }
        heap[index] = he;
    }

    private void trickleDown(int index, HeapEntry he)
    {
        int child = (index * 2) + 1;
        while (child < count)
        {
            if (((child + 1) < count) &&
                (heap[child].Priority > heap[child + 1].Priority))
            {
                child++;
            }
            heap[index] = heap[child];
            index = child;
            child = (index * 2) + 1;
        }
        bubbleUp(index, he);
    }
}