Rotten oranges, by LeetCode

This is apparently a very popular coding interview question: Rotting Oranges - LeetCode

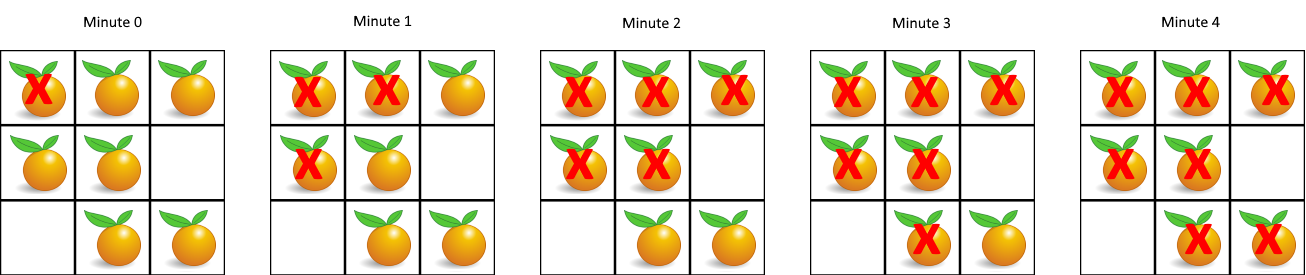
You are given an m x n grid where each cell can have one of three values:

• 0 representing an empty cell,
• 1 representing a fresh orange, or
• 2 representing a rotten orange.

Every minute, any fresh orange that is 4-directionally adjacent to a rotten orange becomes rotten.

Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1.

 

Example 1:

Input: grid = [[2,1,1],[1,1,0],[0,1,1]]
Output: 4

Example 2:

Input: grid = [[2,1,1],[0,1,1],[1,0,1]]
Output: -1
Explanation: The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.

Example 3:

Input: grid = [[0,2]]
Output: 0
Explanation: Since there are already no fresh oranges at minute 0, the answer is just 0.

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 10
• grid[i][j] is 0, 1, or 2.

Accepted

186,480

Submissions

376,397

My approach here is not the fastest, but works. Have a hash table with all the tags that you'll use to identify a rotten orange, starting with 2. In each round, set the good oranges to bad as per the description. This takes N^2 (assuming M=N). Then add the new tag to the hash table. The point of the tagging system is to avoid cascading effects in the same round. The outer loop will be at most N^2. So this turns out to be N^4 with N = 10, or 10K. Small numbers, but I'm sure there is a better, faster implementation. Code is below, stay safe everyone, stay healthy! ACC.

public int OrangesRotting(int[][] grid)
{
    Hashtable rotten = new Hashtable();
    rotten.Add(2, true);

    int nextRotten = 3;
    int minute = 0;
    bool done = false;
    while (!done)
    {
        done = true;
        for (int r = 0; r < grid.Length; r++)
        {
            for (int c = 0; c < grid[r].Length; c++)
            {
                if (grid[r][c] == 1)
                {
                    if ((r - 1 >= 0 && rotten.ContainsKey(grid[r - 1][c])) ||
                        (r + 1 < grid.Length && rotten.ContainsKey(grid[r + 1][c])) ||
                        (c - 1 >= 0 && rotten.ContainsKey(grid[r][c - 1])) ||
                        (c + 1 < grid[r].Length && rotten.ContainsKey(grid[r][c + 1])))
                    {
                        grid[r][c] = nextRotten;
                        done = false;
                    }
                }
            }
        }
        if (!done)
        {
            rotten.Add(nextRotten, true);
            nextRotten++;
            minute++;
        }
    }

    for (int r = 0; r < grid.Length; r++)
    {
        for (int c = 0; c < grid[r].Length; c++)
        {
            if (grid[r][c] == 1)
            {
                return -1;
            }
        }
    }

    return minute;
}