Friday hack on a BST

Not super proud of my solution, but sometimes you need to be pragmatic. Here is the problem: Depth of BST Given Insertion Order - LeetCode

1902. Depth of BST Given Insertion Order

Medium

You are given a 0-indexed integer array order of length n, a permutation of integers from 1 to n representing the order of insertion into a binary search tree.

A binary search tree is defined as follows:

• The left subtree of a node contains only nodes with keys less than the node's key.
• The right subtree of a node contains only nodes with keys greater than the node's key.
• Both the left and right subtrees must also be binary search trees.

The binary search tree is constructed as follows:

• order[0] will be the root of the binary search tree.
• All subsequent elements are inserted as the child of any existing node such that the binary search tree properties hold.

Return the depth of the binary search tree.

A binary tree's depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

 

Example 1:

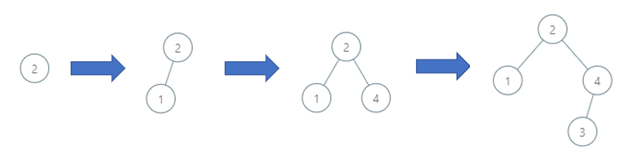
Input: order = [2,1,4,3]
Output: 3
Explanation: The binary search tree has a depth of 3 with path 2->3->4.

Example 2:

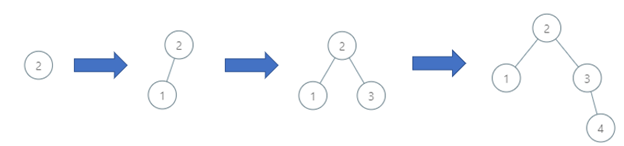
Input: order = [2,1,3,4]
Output: 3
Explanation: The binary search tree has a depth of 3 with path 2->3->4.

Example 3:

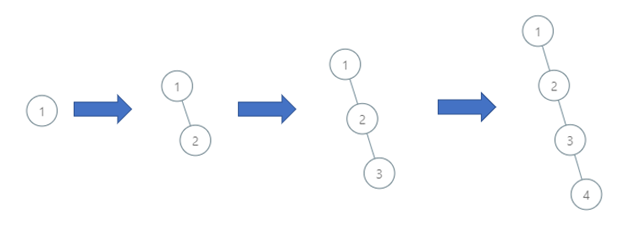
Input: order = [1,2,3,4]
Output: 4
Explanation: The binary search tree has a depth of 4 with path 1->2->3->4.

 

Constraints:

• n == order.length
• 1 <= n <= 105
• order is a permutation of integers between 1 and n.

The solution that I tried was the one expected: add the nodes to the BST, which on average would take NLogN, and keep track of the depth as you're adding the elements. Works, but: TLE. Basically for the case where all the elements are already sorted, the NLogN becomes actually N^2 and since N = 10^5, the N^2 becomes intractable. That's where the ugly hack comes into play: check whether the input array is already sorted. If so, the solution is simply the length of the array. Code is down below, cheers, ACC.

public class TreeNode {
    public int val;
    public TreeNode left;
    public TreeNode right;
    public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
        this.val = val;
        this.left = left;
        this.right = right;
    }

    public void Add(int val, ref int maxDepth)
    {
        this.Add(val, 1, ref maxDepth);
    }

    private void Add(int val, int currentDepth, ref int maxDepth)
    {
        if (val > this.val)
        {
            if (this.right == null)
            {
                maxDepth = Math.Max(maxDepth, currentDepth + 1);
                this.right = new TreeNode(val);
                return;
            }
            else
            {
                this.right.Add(val, currentDepth + 1, ref maxDepth);
            }
        }
        else
        {
            if (this.left == null)
            {
                maxDepth = Math.Max(maxDepth, currentDepth + 1);
                this.left = new TreeNode(val);
                return;
            }
            else
            {
                this.left.Add(val, currentDepth + 1, ref maxDepth);
            }
        }
    }
}

public class Solution {
    public int MaxDepthBST(int[] order)
    {
        if (order.Length > 1)
        {
            if (order[0] > order[1])
            {
                bool sorted = true;
                for (int i = 0; i < order.Length - 1; i++)
                {
                    if (order[i] <= order[i + 1])
                    {
                        sorted = false;
                        break;
                    }
                }
                if (sorted) return order.Length;
            }
            else
            {
                bool sorted = true;
                for (int i = 0; i < order.Length - 1; i++)
                {
                    if (order[i] >= order[i + 1])
                    {
                        sorted = false;
                        break;
                    }
                }
                if (sorted) return order.Length;
            }
        }

        TreeNode tree = new TreeNode(order[0]);
        int depth = 1;
        for (int i = 1; i < order.Length; i++)
        {
            tree.Add(order[i], ref depth);
        }
        return depth;
    }
}