Performing a BFS on all directions in a Binary Tree

I've tried this problem before pre-pandemic and failed to realize that it requires something not very common: to perform a BFS on a binary tree across all directions. The "across all directions" means that it is necessary to create the link node -> parent. This can be done using a simple DFS storing the info in a hash table. Then once you find the node related to K (another DFS), then perform a BFS going left, right, parent. All the code together should run in linear time, with a constant 3 (O(3N)). Code is below, cheers, ACC.

Closest Leaf in a Binary Tree - LeetCode

Given the root of a binary tree where every node has a unique value and a target integer k, return the value of the nearest leaf node to the target k in the tree.

Nearest to a leaf means the least number of edges traveled on the binary tree to reach any leaf of the tree. Also, a node is called a leaf if it has no children.

 

Example 1:

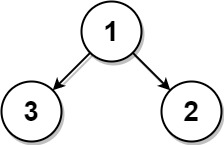
Input: root = [1,3,2], k = 1
Output: 2
Explanation: Either 2 or 3 is the nearest leaf node to the target of 1.

Example 2:

Input: root = [1], k = 1
Output: 1
Explanation: The nearest leaf node is the root node itself.

Example 3:

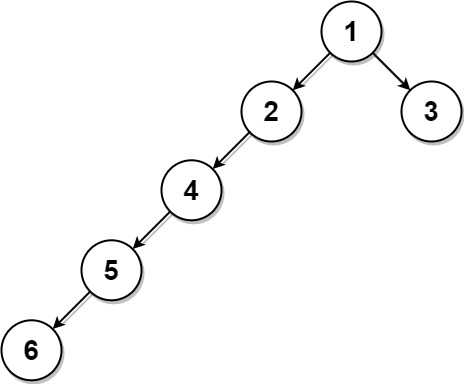
Input: root = [1,2,3,4,null,null,null,5,null,6], k = 2
Output: 3
Explanation: The leaf node with value 3 (and not the leaf node with value 6) is nearest to the node with value 2.

 

Constraints:

• The number of nodes in the tree is in the range [1, 1000].
• 1 <= Node.val <= 1000
• All the values of the tree are unique.
• There exist some node in the tree where Node.val == k.

public class QueueItem
{
    public TreeNode node = null;
    public int steps = 0;

    public QueueItem(TreeNode node, int steps)
    {
        this.node = node;
        this.steps = steps;
    }
}

public class Solution
{
    public int FindClosestLeaf(TreeNode root, int k)
    {
        Hashtable nodeParent = new Hashtable();
        CreateTreeNodeParent(root, null, nodeParent);

        TreeNode target = FindK(root, k);

        //BFS
        Queue queue = new Queue();
        Hashtable visited = new Hashtable();
        QueueItem qi = new QueueItem(target, 0);
        queue.Enqueue(qi);
        visited.Add(target.val, true);

        int minDistance = Int32.MaxValue;
        int minNodeVal = -1;

        while (queue.Count > 0)
        {
            QueueItem currentQi = queue.Dequeue();

            if (currentQi.node != null && currentQi.node.left == null && currentQi.node.right == null)
            {
                if (currentQi.steps < minDistance)
                {
                    minDistance = currentQi.steps;
                    minNodeVal = currentQi.node.val;
                }
            }

            //Children:
            if (currentQi.node.left != null && !visited.ContainsKey(currentQi.node.left.val))
            {
                QueueItem leftQueueItem = new QueueItem(currentQi.node.left, currentQi.steps + 1);
                queue.Enqueue(leftQueueItem);
                visited.Add(currentQi.node.left.val, true);
            }
            if (currentQi.node.right != null && !visited.ContainsKey(currentQi.node.right.val))
            {
                QueueItem rightQueueItem = new QueueItem(currentQi.node.right, currentQi.steps + 1);
                queue.Enqueue(rightQueueItem);
                visited.Add(currentQi.node.right.val, true);
            }

            //Parent:
            TreeNode parent = (TreeNode)nodeParent[currentQi.node.val];
            if (parent != null && !visited.ContainsKey(parent.val))
            {
                QueueItem parentQueueItem = new QueueItem(parent, currentQi.steps + 1);
                queue.Enqueue(parentQueueItem);
                visited.Add(parent.val, true);
            }
        }

        return minNodeVal;
    }

    public TreeNode FindK(TreeNode node, int k)
    {
        if (node != null)
        {
            if (node.val == k) return node;
            TreeNode left = FindK(node.left, k);
            if (left != null) return left;
            TreeNode right = FindK(node.right, k);
            return right;
        }
        else
        {
            return null;
        }
    }

    public void CreateTreeNodeParent(TreeNode node, TreeNode parent, Hashtable nodeParent)
    {
        if (node != null)
        {
            nodeParent.Add(node.val, parent);
            CreateTreeNodeParent(node.left, node, nodeParent);
            CreateTreeNodeParent(node.right, node, nodeParent);
        }
    }
}