Calculating the scores of a binary tree in linear time

This problem was a little more complex than the average medium problem. It can be solved in linear time (and linear space) in 3 steps:

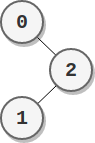
1/ Build the graph and store in a hash table (this will be needed for the next steps). This can be done in O(n) with a linear scan

2/ Count the number of nodes in each subtree. Also O(n) (Post-Order DFS)

3/ Linear scan to calculate the score for each subtree, O(n). Warning: use LONG, since you're dealing with multiplication of 3 integers where each integer may be in the 10^5 range, it will overflow if you're not careful.

Code is down below. Cheers, ACC.

Count Nodes With the Highest Score - LeetCode

2049. Count Nodes With the Highest Score

Medium

There is a binary tree rooted at 0 consisting of n nodes. The nodes are labeled from 0 to n - 1. You are given a 0-indexed integer array parents representing the tree, where parents[i] is the parent of node i. Since node 0 is the root, parents[0] == -1.

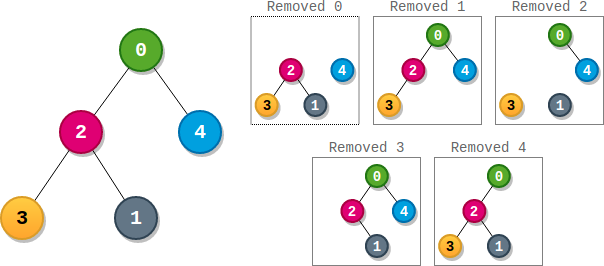
Each node has a score. To find the score of a node, consider if the node and the edges connected to it were removed. The tree would become one or more non-empty subtrees. The size of a subtree is the number of the nodes in it. The score of the node is the product of the sizes of all those subtrees.

Return the number of nodes that have the highest score.

 

Example 1:

Input: parents = [-1,2,0,2,0]
Output: 3
Explanation:
- The score of node 0 is: 3 * 1 = 3
- The score of node 1 is: 4 = 4
- The score of node 2 is: 1 * 1 * 2 = 2
- The score of node 3 is: 4 = 4
- The score of node 4 is: 4 = 4
The highest score is 4, and three nodes (node 1, node 3, and node 4) have the highest score.

Example 2:

Input: parents = [-1,2,0]
Output: 2
Explanation:
- The score of node 0 is: 2 = 2
- The score of node 1 is: 2 = 2
- The score of node 2 is: 1 * 1 = 1
The highest score is 2, and two nodes (node 0 and node 1) have the highest score.

 

Constraints:

• n == parents.length
• 2 <= n <= 105
• parents[0] == -1
• 0 <= parents[i] <= n - 1 for i != 0
• parents represents a valid binary tree.

Accepted

3,109

Submissions

7,386

public int CountHighestScoreNodes(int[] parents)
{
    Hashtable tree = new Hashtable();
    int root = 0;

    //Step 1: build the tree, O(n)-time and O(n)-space
    for (int i = 0; i < parents.Length; i++)
    {
        int c = i;
        int p = parents[i];

        if (!tree.ContainsKey(p)) tree.Add(p, new Hashtable());
        Hashtable children = (Hashtable)tree[p];
        children.Add(c, true);

        if (p == -1) root = c;
    }

    //Step 2: count the number of nodes for each subtree, O(n)-time
    int[] countOfNodes = new int[parents.Length];
    CountNodes(root, tree, ref countOfNodes);

    //Step 3: calculate the scores and store them in a sorted list, O(n)-time, O(n)-space
    //Important! Use LONG since we're dealing with multiplication and may stumble upon overflow!
    SortedList countScores = new SortedList();
    for (int i = 0; i < countOfNodes.Length; i++)
    {
        long parentMultiplier = countOfNodes[root] - countOfNodes[i];
        parentMultiplier = (parentMultiplier == 0) ? 1 : parentMultiplier;

        long childrenMultiplier = 1;
        if (tree.ContainsKey(i))
        {
            Hashtable children = (Hashtable)tree[i];
            foreach (int child in children.Keys)
            {
                childrenMultiplier *= countOfNodes[child];
            }
        }

        long score = parentMultiplier * childrenMultiplier;

        if (!countScores.ContainsKey(score)) countScores.Add(score, 0);
        countScores[score]++;
    }

    return countScores.Last().Value;
}

public int CountNodes(int currentNode,
                        Hashtable tree,
                        ref int[] countOfNodes)
{
    if (!tree.ContainsKey(currentNode))
    {
        countOfNodes[currentNode] = 1;
        return 1;
    }

    int count = 1;
    Hashtable children = (Hashtable)tree[currentNode];
    foreach (int child in children.Keys)
    {
        count += CountNodes(child, tree, ref countOfNodes);
    }
    countOfNodes[currentNode] = count;
    return count;
}