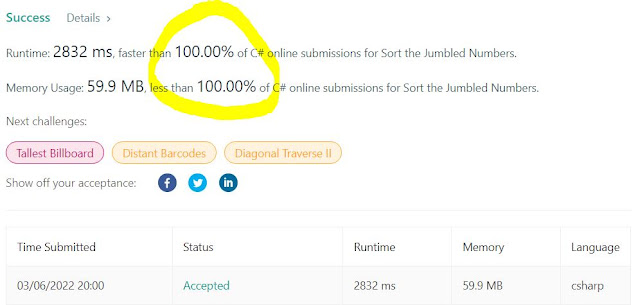
Untying the knot

Let's talk about untying the knot... You're given a fully-connected, undirected graph that contains at most one knot. A knot is defined as a loop. The graph contains only unique positive integers as the edges, and if an edge (a,b) is in the graph, then it is guaranteed that a!=b. The graph may have up to 10^5 nodes. In order to untie the knot, you need to first find the loop (if it exists) in the graph, and then find the smallest element in that loop. In the example below, the graph does have one loop, and the smallest element (the weak link) is node 3. That's what you should return. Otherwise, if there is no loop, return -1. Here is how I solved it: 1/ Created the graph (from the edges) using a hash table (that's my favorite way to handle a graph) 2/ Perform a DFS recursively looking for a loop 3/ As you do the DFS, store the current node and the parent node 4/ Once you find a loop, then backtrack non-recursively in order to find the smallest element 5/ Notice that bec...