All Ancestors: Shallow and Deep Hash tables

This is going to be a recursive solution using DFS, but the difference is that we'll use two hash tables: the first one will be a shallow connection which we'll populate based on the edges input. The second one will contain the full deep connections of all ancestors. This is the one that we want to populate thoroughly throughout the recursive calls. Once we have the deep connections fully populated, then it is just a matter of parsing it and creating the return value. Code is down below, cheers, ACC.

All Ancestors of a Node in a Directed Acyclic Graph - LeetCode

2192. All Ancestors of a Node in a Directed Acyclic Graph

Medium

You are given a positive integer n representing the number of nodes of a Directed Acyclic Graph (DAG). The nodes are numbered from 0 to n - 1 (inclusive).

You are also given a 2D integer array edges, where edges[i] = [fromi, toi] denotes that there is a unidirectional edge from fromi to toi in the graph.

Return a list answer, where answer[i] is the list of ancestors of the ith node, sorted in ascending order.

A node u is an ancestor of another node v if u can reach v via a set of edges.

 

Example 1:

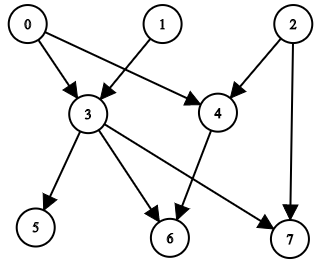
Input: n = 8, edgeList = [[0,3],[0,4],[1,3],[2,4],[2,7],[3,5],[3,6],[3,7],[4,6]]
Output: [[],[],[],[0,1],[0,2],[0,1,3],[0,1,2,3,4],[0,1,2,3]]
Explanation:
The above diagram represents the input graph.
- Nodes 0, 1, and 2 do not have any ancestors.
- Node 3 has two ancestors 0 and 1.
- Node 4 has two ancestors 0 and 2.
- Node 5 has three ancestors 0, 1, and 3.
- Node 6 has five ancestors 0, 1, 2, 3, and 4.
- Node 7 has four ancestors 0, 1, 2, and 3.

Example 2:

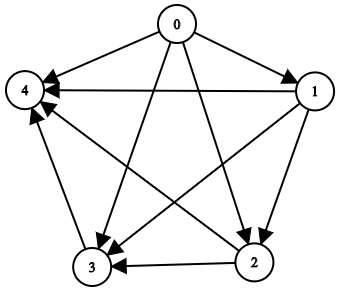
Input: n = 5, edgeList = [[0,1],[0,2],[0,3],[0,4],[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]]
Output: [[],[0],[0,1],[0,1,2],[0,1,2,3]]
Explanation:
The above diagram represents the input graph.
- Node 0 does not have any ancestor.
- Node 1 has one ancestor 0.
- Node 2 has two ancestors 0 and 1.
- Node 3 has three ancestors 0, 1, and 2.
- Node 4 has four ancestors 0, 1, 2, and 3.

 

Constraints:

• 1 <= n <= 1000
• 0 <= edges.length <= min(2000, n * (n - 1) / 2)
• edges[i].length == 2
• 0 <= fromi, toi <= n - 1
• fromi != toi
• There are no duplicate edges.
• The graph is directed and acyclic.

public IList> GetAncestors(int n, int[][] edges)
{
    Hashtable nodeToSortedListAncestorsShallow = new Hashtable();

    for (int i = 0; i < edges.Length; i++)
    {
        if (!nodeToSortedListAncestorsShallow.ContainsKey(edges[i][1]))
        {
            nodeToSortedListAncestorsShallow.Add(edges[i][1], new SortedList());
        }
        SortedList sortedList = (SortedList)nodeToSortedListAncestorsShallow[edges[i][1]];
        if (!sortedList.ContainsKey(edges[i][0])) sortedList.Add(edges[i][0], edges[i][0]);
    }

    Hashtable nodeToSortedListAncestorsDeep = new Hashtable();
    for (int i = 0; i < n; i++)
    {
        GetAncestors(i, nodeToSortedListAncestorsShallow, nodeToSortedListAncestorsDeep);
    }

    List> retVal = new List>();
    for (int i = 0; i < n; i++)
    {
        if (!nodeToSortedListAncestorsDeep.ContainsKey(i))
        {
            retVal.Add(new List());
        }
        else
        {
            SortedList sortedList = (SortedList)nodeToSortedListAncestorsDeep[i];
            List list = new List();
            foreach (int k in sortedList.Keys) list.Add(k);
            retVal.Add(list);
        }
    }

    return retVal;
}

private void GetAncestors(int node, 
                            Hashtable nodeToSortedListAncestorsShallow,
                            Hashtable nodeToSortedListAncestorsDeep)
{
    if (nodeToSortedListAncestorsDeep.ContainsKey(node)) return;

    nodeToSortedListAncestorsDeep.Add(node, new SortedList());
    SortedList sortedList = (SortedList)nodeToSortedListAncestorsDeep[node];

    if (nodeToSortedListAncestorsShallow.ContainsKey(node))
    {
        SortedList nodes = (SortedList)nodeToSortedListAncestorsShallow[node];
        foreach (int n in nodes.Keys)
        {
            if (!sortedList.ContainsKey(n)) sortedList.Add(n, n);
            if (!nodeToSortedListAncestorsDeep.ContainsKey(n))
            {
                GetAncestors(n, nodeToSortedListAncestorsShallow, nodeToSortedListAncestorsDeep);
            }
            if (nodeToSortedListAncestorsDeep.ContainsKey(n))
            {
                SortedList toCopy = (SortedList)nodeToSortedListAncestorsDeep[n];
                foreach (int m in toCopy.Keys)
                {
                    if (!sortedList.Contains(m)) sortedList.Add(m, m);
                }
            }
        }
    }
}