Create Binary Tree from Descriptions: Tail Recursion

This problem is a simple parser of the input data structure, placing it in a hashtable (the "graph") followed by a tail recursion. Tail recursion happens when the recursive call is the last statement in the function. It can easily be modified by using a stack, de-recursifying a function, this is usually well done by functional languages. In my case, I kept the recursive calls. Code is down below, cheers, ACC.

Create Binary Tree From Descriptions - LeetCode

2196. Create Binary Tree From Descriptions

Medium

You are given a 2D integer array descriptions where descriptions[i] = [parenti, childi, isLefti] indicates that parenti is the parent of childi in a binary tree of unique values. Furthermore,

• If isLefti == 1, then childi is the left child of parenti.
• If isLefti == 0, then childi is the right child of parenti.

Construct the binary tree described by descriptions and return its root.

The test cases will be generated such that the binary tree is valid.

 

Example 1:

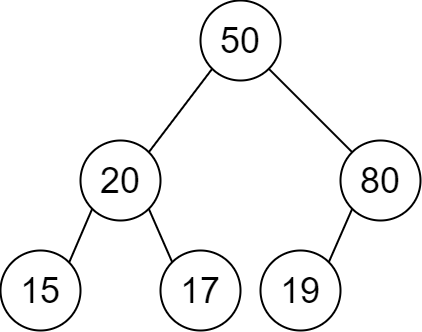
Input: descriptions = [[20,15,1],[20,17,0],[50,20,1],[50,80,0],[80,19,1]]
Output: [50,20,80,15,17,19]
Explanation: The root node is the node with value 50 since it has no parent.
The resulting binary tree is shown in the diagram.

Example 2:

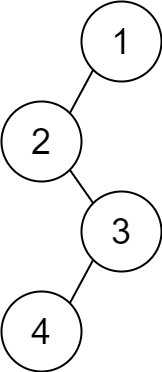
Input: descriptions = [[1,2,1],[2,3,0],[3,4,1]]
Output: [1,2,null,null,3,4]
Explanation: The root node is the node with value 1 since it has no parent.
The resulting binary tree is shown in the diagram.

 

Constraints:

• 1 <= descriptions.length <= 104
• descriptions[i].length == 3
• 1 <= parenti, childi <= 105
• 0 <= isLefti <= 1
• The binary tree described by descriptions is valid.

public TreeNode CreateBinaryTree(int[][] descriptions)
{
    Hashtable allNumbers = new Hashtable();
    Hashtable graph = new Hashtable();

    for (int i = 0; i < descriptions.Length; i++)
    {
        int parent = descriptions[i][0];
        int child = descriptions[i][1];
        bool isLeft = (descriptions[i][2] == 1);

        if (!allNumbers.ContainsKey(parent)) allNumbers.Add(parent, false);

        if (!allNumbers.ContainsKey(child)) allNumbers.Add(child, true);
        else allNumbers[child] = true;

        if (!graph.ContainsKey(parent)) graph.Add(parent, new Hashtable());
        Hashtable children = (Hashtable)graph[parent];
        if (!children.ContainsKey(child)) children.Add(child, isLeft);
    }

    //Find root
    int root = 0;
    foreach (int n in allNumbers.Keys)
    {
        if (!(bool)allNumbers[n])
        {
            root = n;
            break;
        }
    }

    TreeNode tree = new TreeNode(root);
    CreateBinaryTree(root, graph, tree);
    return tree;
}

private void CreateBinaryTree(int node, 
                                Hashtable graph,
                                TreeNode tree)
{
    if (!graph.ContainsKey(node)) return;

    Hashtable children = (Hashtable)graph[node];
    foreach (int child in children.Keys)
    {
        bool isLeft = (bool)children[child];

        if (isLeft)
        {
            tree.left = new TreeNode(child);
            CreateBinaryTree(child, graph, tree.left);
        }
        else
        {
            tree.right = new TreeNode(child);
            CreateBinaryTree(child, graph, tree.right);
        }
    }
}