Importance of Roads: P-Queue in Action

Not super fast solution here, pretty much O(nlogn) for an N=10^4, using pQueue. Here is the gist of it:

1/ It is a graph problem where you need to assign the largest number to the node with the most number of connections

2/ Use a hash table to implement the graph (hash of hash)

3/ Build the graph using #2

4/ Using a pQueue (descended order), add the cities based on the number of connections (as the weight)

5/ Dequeue and assign the different values for the cities ([n..1])

6/ Traverse the graph again adding up the importance. Need to ensure that the same road isn't counted twice (another hash table of "visited")

Code is down below, cheers, ACC.

Maximum Total Importance of Roads - LeetCode

2285. Maximum Total Importance of Roads

Medium

You are given an integer n denoting the number of cities in a country. The cities are numbered from 0 to n - 1.

You are also given a 2D integer array roads where roads[i] = [ai, bi] denotes that there exists a bidirectional road connecting cities ai and bi.

You need to assign each city with an integer value from 1 to n, where each value can only be used once. The importance of a road is then defined as the sum of the values of the two cities it connects.

Return the maximum total importance of all roads possible after assigning the values optimally.

 

Example 1:

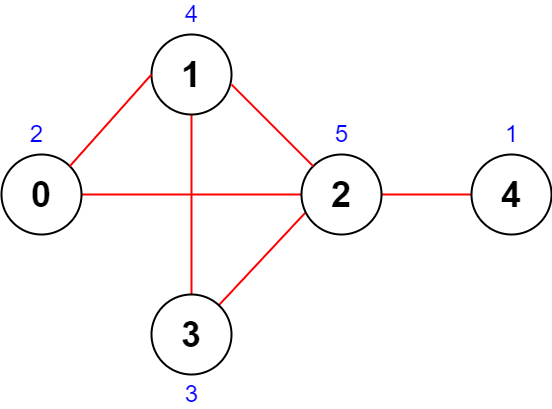
Input: n = 5, roads = [[0,1],[1,2],[2,3],[0,2],[1,3],[2,4]]
Output: 43
Explanation: The figure above shows the country and the assigned values of [2,4,5,3,1].
- The road (0,1) has an importance of 2 + 4 = 6.
- The road (1,2) has an importance of 4 + 5 = 9.
- The road (2,3) has an importance of 5 + 3 = 8.
- The road (0,2) has an importance of 2 + 5 = 7.
- The road (1,3) has an importance of 4 + 3 = 7.
- The road (2,4) has an importance of 5 + 1 = 6.
The total importance of all roads is 6 + 9 + 8 + 7 + 7 + 6 = 43.
It can be shown that we cannot obtain a greater total importance than 43.

Example 2:

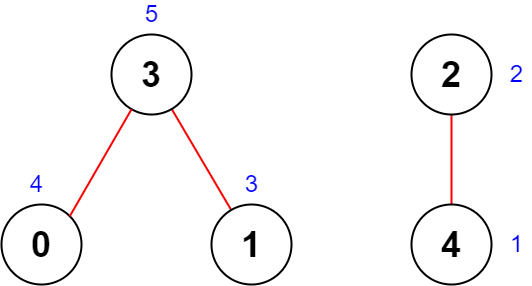
Input: n = 5, roads = [[0,3],[2,4],[1,3]]
Output: 20
Explanation: The figure above shows the country and the assigned values of [4,3,2,5,1].
- The road (0,3) has an importance of 4 + 5 = 9.
- The road (2,4) has an importance of 2 + 1 = 3.
- The road (1,3) has an importance of 3 + 5 = 8.
The total importance of all roads is 9 + 3 + 8 = 20.
It can be shown that we cannot obtain a greater total importance than 20.

 

Constraints:

• 2 <= n <= 5 * 104
• 1 <= roads.length <= 5 * 104
• roads[i].length == 2
• 0 <= ai, bi <= n - 1
• ai != bi
• There are no duplicate roads.

Accepted

11,482

Submissions

19,494

public class Solution {
    public long MaximumImportance(int n, int[][] roads)
    {
        Hashtable graph = new Hashtable();

        //O(n): creation of the graph
        for (int i = 0; i < roads.Length; i++)
        {
            for (int j = 0; j < 2; j++)
            {
                if (!graph.ContainsKey(roads[i][j])) graph.Add(roads[i][j], new Hashtable());
                Hashtable connections = (Hashtable)graph[roads[i][j]];
                if (!connections.ContainsKey(roads[i][(j + 1) % 2])) connections.Add(roads[i][(j + 1) % 2], true);
            }
        }

        //O(nlogn): priority queue sorting (heap sort)
        PriorityQueue pQueue = new PriorityQueue(false);
        foreach (int r in graph.Keys)
        {
            Hashtable connections = (Hashtable)graph[r];
            pQueue.Enqueue(r, connections.Count);
        }

        //O(nlogn): dequeuing and assignement of city numbers
        int[] cityNumber = new int[n];
        int val = n;
        while (pQueue.Count > 0)
        {
            double temp = 0;
            int city = (int)pQueue.Dequeue(out temp);
            cityNumber[city] = val;
            val--;
        }

        //O(n): calculation of ret val based on roads visited
        Hashtable roadVisited = new Hashtable();
        long retVal = 0;
        foreach (int a in graph.Keys)
        {
            Hashtable connections = (Hashtable)graph[a];
            foreach (int b in connections.Keys)
            {
                long key = 100000 * Math.Max(a, b) + Math.Min(a, b);
                if (!roadVisited.ContainsKey(key))
                {
                    retVal += cityNumber[a] + cityNumber[b];
                    roadVisited.Add(key, true);
                }
            }
        }

        return retVal;
    }
}

public class PriorityQueue
{
    public struct HeapEntry
    {
        private object item;
        private double priority;
        public HeapEntry(object item, double priority)
        {
            this.item = item;
            this.priority = priority;
        }
        public object Item
        {
            get
            {
                return item;
            }
        }
        public double Priority
        {
            get
            {
                return priority;
            }
        }
    }

    private bool ascend;
    private int count;
    private int capacity;
    private HeapEntry[] heap;

    public int Count
    {
        get
        {
            return this.count;
        }
    }

    public PriorityQueue(bool ascend)
    {
        capacity = 1000000;
        heap = new HeapEntry[capacity];
        this.ascend = ascend;
    }

    public object Dequeue(out double priority)
    {
        priority = heap[0].Priority;
        object result = heap[0].Item;
        count--;
        trickleDown(0, heap[count]);
        return result;
    }

    public object Peak(/*out double priority*/)
    {
        //priority = heap[0].Priority;
        object result = heap[0].Item;
        return result;
    }

    public void Enqueue(object item, double priority)
    {
        count++;
        bubbleUp(count - 1, new HeapEntry(item, priority));
    }

    private void bubbleUp(int index, HeapEntry he)
    {
        int parent = (index - 1) / 2;
        // note: (index > 0) means there is a parent
        if (this.ascend)
        {
            while ((index > 0) && (heap[parent].Priority > he.Priority))
            {
                heap[index] = heap[parent];
                index = parent;
                parent = (index - 1) / 2;
            }
            heap[index] = he;
        }
        else
        {
            while ((index > 0) && (heap[parent].Priority < he.Priority))
            {
                heap[index] = heap[parent];
                index = parent;
                parent = (index - 1) / 2;
            }
            heap[index] = he;
        }
    }

    private void trickleDown(int index, HeapEntry he)
    {
        int child = (index * 2) + 1;
        while (child < count)
        {
            if (this.ascend)
            {
                if (((child + 1) < count) &&
                    (heap[child].Priority > heap[child + 1].Priority))
                {
                    child++;
                }
            }
            else
            {
                if (((child + 1) < count) &&
                    (heap[child].Priority < heap[child + 1].Priority))
                {
                    child++;
                }
            }
            heap[index] = heap[child];
            index = child;
            child = (index * 2) + 1;
        }
        bubbleUp(index, he);
    }
}