On a quick implementation of GCD - Greatest Common Divisor

This problem interestingly enough requires a quick implementation of the millennium-old GCD - Greatest Common Divisor. It is a geometric problem where what you need to do is check whether point V2 belongs to the same line as points V1 and V0. In order to do so, and to avoid floating-point arithmetic, keep track of the slope of V1 and V0 using the num/den fraction, but reduce it to its irreducible form. In order to do so, you'll need to calculate the GCD between num and den. That can be done using Euclid's algorithm which runs in LogN. Since there is a sorting pre-step involved, the total execution time would be NLogN. Code is down below, cheers, ACC.

Minimum Lines to Represent a Line Chart - LeetCode

2280. Minimum Lines to Represent a Line Chart

Medium

You are given a 2D integer array stockPrices where stockPrices[i] = [dayi, pricei] indicates the price of the stock on day dayi is pricei. A line chart is created from the array by plotting the points on an XY plane with the X-axis representing the day and the Y-axis representing the price and connecting adjacent points. One such example is shown below:

Return the minimum number of lines needed to represent the line chart.

 

Example 1:

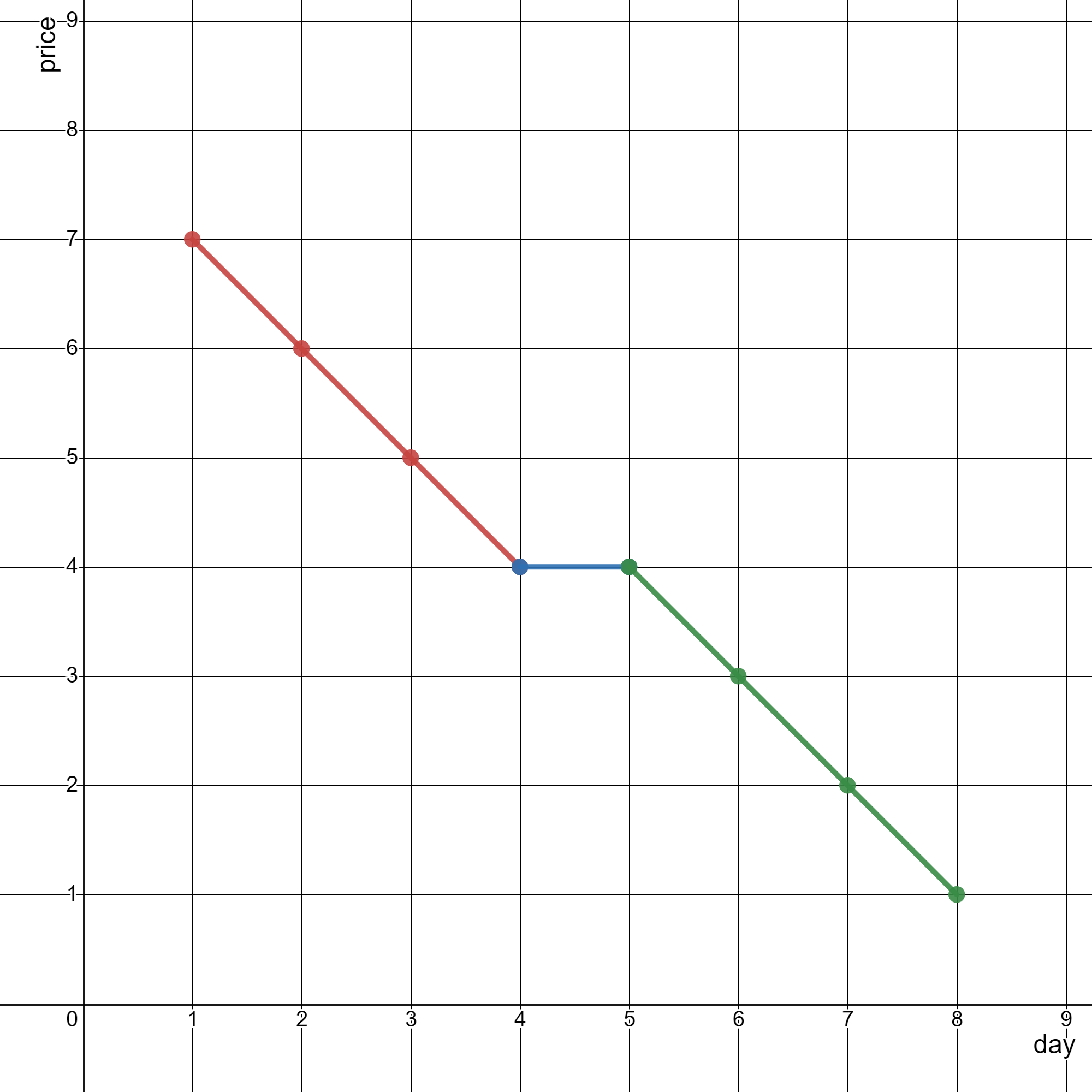
Input: stockPrices = [[1,7],[2,6],[3,5],[4,4],[5,4],[6,3],[7,2],[8,1]]
Output: 3
Explanation:
The diagram above represents the input, with the X-axis representing the day and Y-axis representing the price.
The following 3 lines can be drawn to represent the line chart:
- Line 1 (in red) from (1,7) to (4,4) passing through (1,7), (2,6), (3,5), and (4,4).
- Line 2 (in blue) from (4,4) to (5,4).
- Line 3 (in green) from (5,4) to (8,1) passing through (5,4), (6,3), (7,2), and (8,1).
It can be shown that it is not possible to represent the line chart using less than 3 lines.

Example 2:

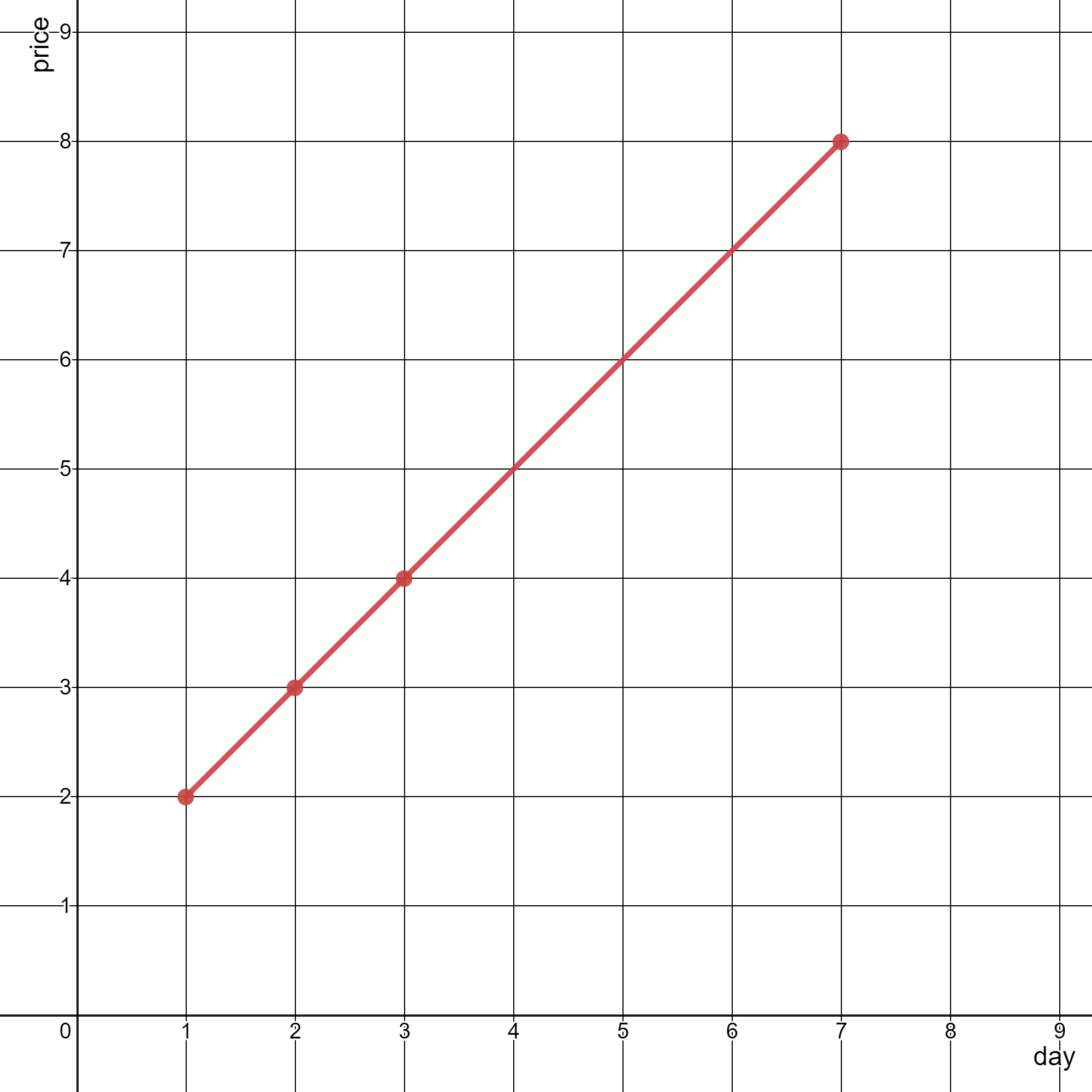
Input: stockPrices = [[3,4],[1,2],[7,8],[2,3]]
Output: 1
Explanation:
As shown in the diagram above, the line chart can be represented with a single line.

 

Constraints:

• 1 <= stockPrices.length <= 105
• stockPrices[i].length == 2
• 1 <= dayi, pricei <= 109
• All dayi are distinct.

Accepted

11,861

Submissions

57,474

public class Solution
{
    public class MyComparerStocks : IComparer
    {
        public int Compare(Object x, Object y)
        {
            int[] dayStock1 = (int[])x;
            int[] dayStock2 = (int[])y;

            return dayStock1[0].CompareTo(dayStock2[0]);
        }
    }
    public int MinimumLines(int[][] stockPrices)
    {
        if (stockPrices.Length <= 1) return 0;

        Array.Sort(stockPrices, new MyComparerStocks());

        Hashtable cache = new Hashtable();

        int retVal = 1;
        int distX = stockPrices[1][0] - stockPrices[0][0];
        int distY = stockPrices[1][1] - stockPrices[0][1];
        int prevNum = 0;
        int prevDen = 0;
        SimplifyFraction(distX, distY, ref prevNum, ref prevDen);

        for (int i = 2; i < stockPrices.Length; i++)
        {
            distX = stockPrices[i][0] - stockPrices[i - 1][0];
            distY = stockPrices[i][1] - stockPrices[i - 1][1];
            int currNum = 0;
            int currDen = 0;
            SimplifyFraction(distX, distY, ref currNum, ref currDen);

            if (prevNum != currNum || prevDen != currDen) retVal++;
            prevNum = currNum;
            prevDen = currDen;
        }

        return retVal;
    }

    private void SimplifyFraction(int a,
                                    int b,
                                    ref int num,
                                    ref int den)
    {
        num = Math.Abs(a);
        den = Math.Abs(b);

        int mul = 1;
        if ((a < 0 && b > 0) || (a > 0 && b < 0)) mul = -1;

        int gcd = GCD(num, den);
        while (gcd > 1)
        {
            num /= gcd;
            den /= gcd;

            gcd = GCD(num, den);
        }

        num *= mul;
    }
    private int GCD(int a, int b)
    {
        while (a != 0 && b != 0)
        {
            if (a > b)
                a %= b;
            else
                b %= a;
        }

        return a == 0 ? b : a;
    }
}

And Happy 15th birthday to my beloved little girl!!!!!!!