The power of pruning in backtracking

This problem, given the small constraints and the hint, is asking to generate all the possibilities. The recursion becomes exponential fairly quickly. Basically at each iteration, you have to:

1/ Simulate adding the current cookie to the current child, and recursive to the next child

2/ Simulate adding the current cookie to the current child, and recursive to the current child

3/ Simulate skipping adding at all, and go to the next child

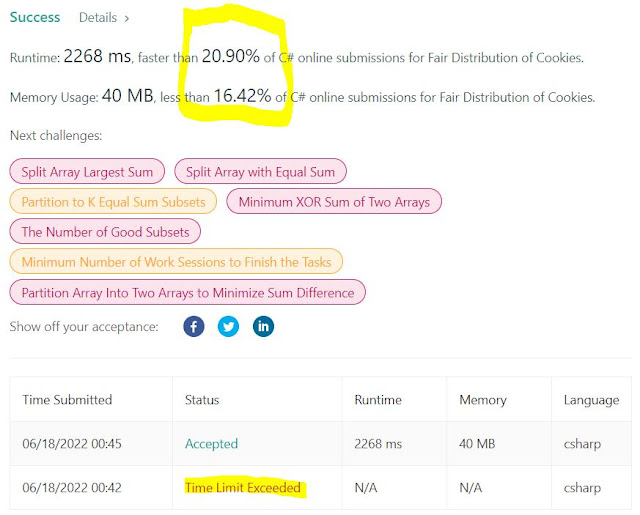
In order to avoid TLE like it happened below, add the following pruning rule:

a/ The moment that the unfairnness is higher than the min, return and break the search

That does the trick. Code is down below, cheers, ACC.

Fair Distribution of Cookies - LeetCode

2305. Fair Distribution of Cookies

Medium

You are given an integer array cookies, where cookies[i] denotes the number of cookies in the ith bag. You are also given an integer k that denotes the number of children to distribute all the bags of cookies to. All the cookies in the same bag must go to the same child and cannot be split up.

The unfairness of a distribution is defined as the maximum total cookies obtained by a single child in the distribution.

Return the minimum unfairness of all distributions.

 

Example 1:

Input: cookies = [8,15,10,20,8], k = 2
Output: 31
Explanation: One optimal distribution is [8,15,8] and [10,20]
- The 1st child receives [8,15,8] which has a total of 8 + 15 + 8 = 31 cookies.
- The 2nd child receives [10,20] which has a total of 10 + 20 = 30 cookies.
The unfairness of the distribution is max(31,30) = 31.
It can be shown that there is no distribution with an unfairness less than 31.

Example 2:

Input: cookies = [6,1,3,2,2,4,1,2], k = 3
Output: 7
Explanation: One optimal distribution is [6,1], [3,2,2], and [4,1,2]
- The 1st child receives [6,1] which has a total of 6 + 1 = 7 cookies.
- The 2nd child receives [3,2,2] which has a total of 3 + 2 + 2 = 7 cookies.
- The 3rd child receives [4,1,2] which has a total of 4 + 1 + 2 = 7 cookies.
The unfairness of the distribution is max(7,7,7) = 7.
It can be shown that there is no distribution with an unfairness less than 7.

 

Constraints:

• 2 <= cookies.length <= 8
• 1 <= cookies[i] <= 105
• 2 <= k <= cookies.length

Accepted

10,892

Submissions

17,380

public int DistributeCookies(int[] cookies, int k)
{
    int[] cummulativeCookies = new int[k];
    int retVal = Int32.MaxValue;

    DistributeCookies(cookies,
                        cummulativeCookies,
                        0,
                        new Hashtable(),
                        ref retVal);

    return retVal;
}

private bool DistributeCookies(int[] cookies,
                                int[] cummulativeCookies,
                                int indexK,
                                Hashtable usedCookies,
                                ref int minUnfairness)
{
    if (cummulativeCookies.Max() >= minUnfairness) return false;
    if (indexK >= cummulativeCookies.Length)
    {
        if (usedCookies.Count == cookies.Length)
        {
            /*
            Console.WriteLine("IndexK = {0}", indexK);
            foreach (int i in usedCookies.Keys) Console.Write("{0} ", i);
            Console.WriteLine();
            foreach (int c in cummulativeCookies) Console.Write("{0} ", c);
            Console.WriteLine();
            */

            minUnfairness = Math.Min(minUnfairness, cummulativeCookies.Max());
        }
        return true;
    }

    for (int i = 0; i < cookies.Length; i++)
    {
        if (!usedCookies.ContainsKey(i))
        {
            //Add to the current one, and call for the next ones
            usedCookies.Add(i, true);
            cummulativeCookies[indexK] += cookies[i];
            bool cont = DistributeCookies(cookies,
                                            cummulativeCookies,
                                            indexK + 1,
                                            usedCookies,
                                            ref minUnfairness);
            cummulativeCookies[indexK] -= cookies[i];
            usedCookies.Remove(i);

            if (!cont) break;

            //Add for the current one, and call for the current one
            usedCookies.Add(i, true);
            cummulativeCookies[indexK] += cookies[i];
            cont = DistributeCookies(cookies,
                                        cummulativeCookies,
                                        indexK,
                                        usedCookies,
                                        ref minUnfairness);
            cummulativeCookies[indexK] -= cookies[i];
            usedCookies.Remove(i);

            if (!cont) break;

            //Skip adding it, go to the next one
            cont = DistributeCookies(cookies,
                                        cummulativeCookies,
                                        indexK + 1,
                                        usedCookies,
                                        ref minUnfairness);

            if (!cont) break;
        }
    }

    return true;
}