Reversing odd levels of a Binary Tree - standard BFS

Standard BFS for this problem: keep a list of all the odd elements and whenever you switch state (meaning moving to an even level - reminds me of a little bit of FSM), then you can "reverse the list". Make sure to do one more time outside of the main queue loop for the case where the last level is an odd one. Code is down below, cheers, ACC.

Reverse Odd Levels of Binary Tree - LeetCode

2415. Reverse Odd Levels of Binary Tree

Medium

Given the root of a perfect binary tree, reverse the node values at each odd level of the tree.

• For example, suppose the node values at level 3 are [2,1,3,4,7,11,29,18], then it should become [18,29,11,7,4,3,1,2].

Return the root of the reversed tree.

A binary tree is perfect if all parent nodes have two children and all leaves are on the same level.

The level of a node is the number of edges along the path between it and the root node.

 

Example 1:

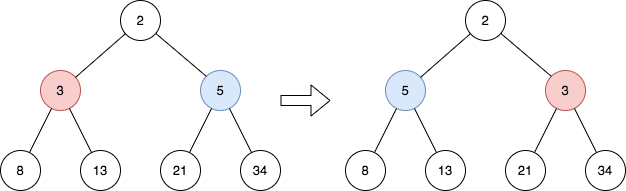
Input: root = [2,3,5,8,13,21,34]
Output: [2,5,3,8,13,21,34]
Explanation: 
The tree has only one odd level.
The nodes at level 1 are 3, 5 respectively, which are reversed and become 5, 3.

Example 2:

Input: root = [7,13,11]
Output: [7,11,13]
Explanation: 
The nodes at level 1 are 13, 11, which are reversed and become 11, 13.

Example 3:

Input: root = [0,1,2,0,0,0,0,1,1,1,1,2,2,2,2]
Output: [0,2,1,0,0,0,0,2,2,2,2,1,1,1,1]
Explanation: 
The odd levels have non-zero values.
The nodes at level 1 were 1, 2, and are 2, 1 after the reversal.
The nodes at level 3 were 1, 1, 1, 1, 2, 2, 2, 2, and are 2, 2, 2, 2, 1, 1, 1, 1 after the reversal.

 

Constraints:

• The number of nodes in the tree is in the range [1, 214].
• 0 <= Node.val <= 105
• root is a perfect binary tree.

Accepted

13,597

Submissions

17,862

public class TreeNodeOddQueueItem
{
    public TreeNode node = null;
    public int level = 0;

    public TreeNodeOddQueueItem(TreeNode node, int level)
    {
        this.node = node;
        this.level = level;
    }
}
public TreeNode ReverseOddLevels(TreeNode root)
{
    if (root == null) return root;
    Queue queue = new Queue();
    TreeNodeOddQueueItem item = new TreeNodeOddQueueItem(root, 0);
    queue.Enqueue(item);

    List list = null;
    while (queue.Count > 0)
    {
        TreeNodeOddQueueItem current = queue.Dequeue();

        if (current.level % 2 == 1)
        {
            if (list == null) list = new List();
            list.Add(current.node);
        }
        else
        {
            if (list != null)
            {
                int leftIndex = 0;
                int rightIndex = list.Count - 1;
                while (leftIndex < rightIndex)
                {
                    int temp = list[leftIndex].val;
                    list[leftIndex].val = list[rightIndex].val;
                    list[rightIndex].val = temp;

                    leftIndex++;
                    rightIndex--;
                }
            }
            list = null;
        }

        if (current.node.left != null) queue.Enqueue(new TreeNodeOddQueueItem(current.node.left, current.level + 1));
        if (current.node.right != null) queue.Enqueue(new TreeNodeOddQueueItem(current.node.right, current.level + 1));
    }

    if (list != null)
    {
        int leftIndex = 0;
        int rightIndex = list.Count - 1;
        while (leftIndex < rightIndex)
        {
            int temp = list[leftIndex].val;
            list[leftIndex].val = list[rightIndex].val;
            list[rightIndex].val = temp;

            leftIndex++;
            rightIndex--;
        }
    }

    return root;
}