The power of pruning in backtracking II

This problem is a little confusing to understand, but it fit with backtracking especially given the small constraints (numbers are small). Backtrack the set of columns to choose, and calculate the rows that fit the coverage. The only pruning is just the beginning of the inner loop where we pass the startIndex in order to avoid starting all over all the time. Code is down below, cheers, ACC.

Maximum Rows Covered by Columns - LeetCode

2397. Maximum Rows Covered by Columns

Medium

You are given a 0-indexed m x n binary matrix mat and an integer cols, which denotes the number of columns you must choose.

A row is covered by a set of columns if each cell in the row that has a value of 1 also lies in one of the columns of the chosen set.

Return the maximum number of rows that can be covered by a set of cols columns.

 

Example 1:

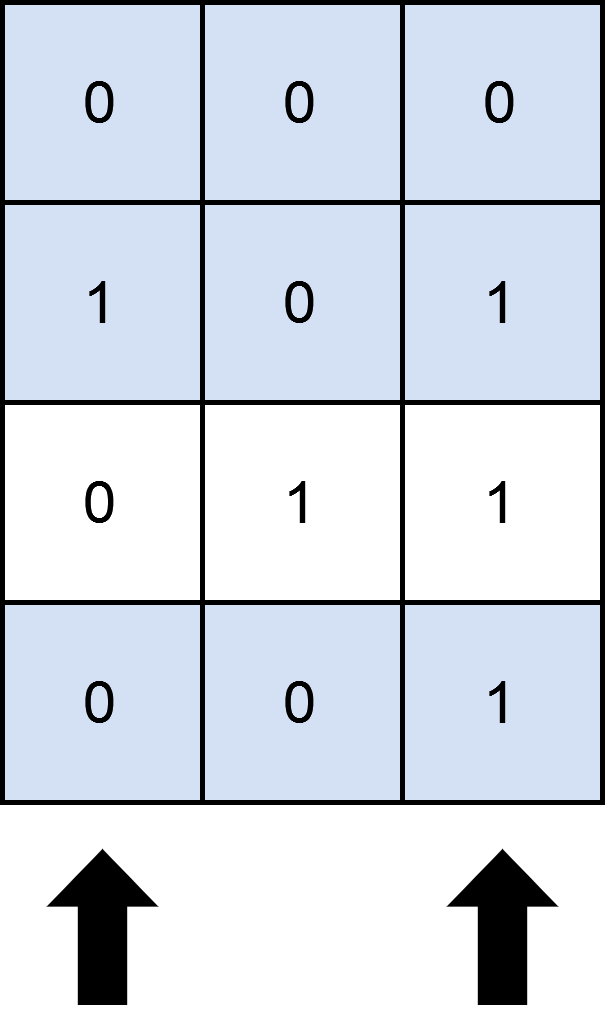
Input: mat = [[0,0,0],[1,0,1],[0,1,1],[0,0,1]], cols = 2
Output: 3
Explanation:
As shown in the diagram above, one possible way of covering 3 rows is by selecting the 0th and 2nd columns.
It can be shown that no more than 3 rows can be covered, so we return 3.

Example 2:

Input: mat = [[1],[0]], cols = 1
Output: 2
Explanation:
Selecting the only column will result in both rows being covered, since the entire matrix is selected.
Therefore, we return 2.

 

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 12
• mat[i][j] is either 0 or 1.
• 1 <= cols <= n

Accepted

6,470

Submissions

14,115

public int MaximumRows(int[][] mat, int cols)
{
    int retVal = 0;
    ProcessMaximumRows(cols, 0, new Hashtable(), mat, ref retVal);
    return retVal;
}

private void ProcessMaximumRows(int cols,
                                int startIndex,
                                Hashtable chosenCols,
                                int[][] mat,
                                ref int max)
{
    if (chosenCols.Count == cols)
    {
        int current = 0;
        for (int r = 0; r < mat.Length; r++)
        {
            bool validRow = true;
            for (int c = 0; c < mat[r].Length; c++)
            {
                if (mat[r][c] == 1 && !chosenCols.ContainsKey(c))
                {
                    validRow = false;
                    break;
                }
            }

            if (validRow) current++;
        }
        max = Math.Max(max, current);
    }

    for (int c = startIndex; c < mat[0].Length; c++)
    {
        if (!chosenCols.ContainsKey(c))
        {
            chosenCols.Add(c, true);
            ProcessMaximumRows(cols, c + 1, chosenCols, mat, ref max);
            chosenCols.Remove(c);
        }
    }
}