In-Order Traversal and Binary Search

This problem requires an in-order traversal of a BST (Binary Search Tree), which keeps the elements of the tree in the same order (sorted), followed by a slight variation of a standard binary search in an array. Code is down below, cheers, ACC.

Closest Nodes Queries in a Binary Search Tree - LeetCode

2476. Closest Nodes Queries in a Binary Search Tree

Medium

You are given the root of a binary search tree and an array queries of size n consisting of positive integers.

Find a 2D array answer of size n where answer[i] = [mini, maxi]:

• mini is the largest value in the tree that is smaller than or equal to queries[i]. If a such value does not exist, add -1 instead.
• maxi is the smallest value in the tree that is greater than or equal to queries[i]. If a such value does not exist, add -1 instead.

Return the array answer.

 

Example 1:

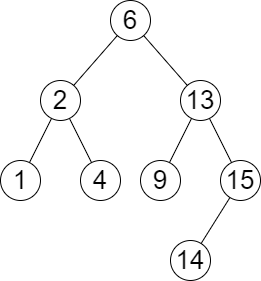
Input: root = [6,2,13,1,4,9,15,null,null,null,null,null,null,14], queries = [2,5,16]
Output: [[2,2],[4,6],[15,-1]]
Explanation: We answer the queries in the following way:
- The largest number that is smaller or equal than 2 in the tree is 2, and the smallest number that is greater or equal than 2 is still 2. So the answer for the first query is [2,2].
- The largest number that is smaller or equal than 5 in the tree is 4, and the smallest number that is greater or equal than 5 is 6. So the answer for the second query is [4,6].
- The largest number that is smaller or equal than 16 in the tree is 15, and the smallest number that is greater or equal than 16 does not exist. So the answer for the third query is [15,-1].

Example 2:

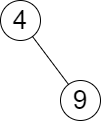
Input: root = [4,null,9], queries = [3]
Output: [[-1,4]]
Explanation: The largest number that is smaller or equal to 3 in the tree does not exist, and the smallest number that is greater or equal to 3 is 4. So the answer for the query is [-1,4].

 

Constraints:

• The number of nodes in the tree is in the range [2, 105].
• 1 <= Node.val <= 106
• n == queries.length
• 1 <= n <= 105
• 1 <= queries[i] <= 106

public IList> ClosestNodes(TreeNode root, IList queries)
{
    List list = new List();
    BSTToList(root, list);
    int[] arr = list.ToArray();

    List> retVal = new List>();

    foreach(int q in queries)
    {
        int min = -1;
        int max = -1;
        BinarySearch(arr, q, ref min, ref max);
        retVal.Add(new List { min, max });
    }

    return retVal;
}

private void BinarySearch(int[] arr,
                            int value,
                            ref int min,
                            ref int max)
{
    min = -1;
    max = -1;

    int left = 0;
    int right = arr.Length - 1;
    while (left < right)
    {
        int middle = (left + right) / 2;
        if (arr[middle] == value)
        {
            min = arr[middle];
            max = arr[middle];
            return;
        }
        else if (arr[middle] > value)
        {
            right = middle - 1;
        }
        else
        {
            left = middle + 1;
        }
    }

    if (arr[left] == value)
    {
        min = arr[left];
        max = arr[left];
    }
    else
    {
        if (arr[left] < value) min = arr[left];
        else if (left - 1 >= 0) min = arr[left - 1];
        if (arr[left] > value) max = arr[left];
        else if (left + 1 < arr.Length) max = arr[left + 1];
    }
}

private void BSTToList(TreeNode node, List list)
{
    if (node == null) return;
    BSTToList(node.left, list);
    list.Add(node.val);
    BSTToList(node.right, list);
}