Trees, Priority Queue, Hash Tables and DFS all at once

Problem here is a Tree problem but the solution requires multiple steps. First, using a DFS create the sum of levels and store in a Hash Table. Then, push the content to a Priority Queue. Finally, dequeue in order to find your answer. Code is down below, cheers, ACC.

2583. Kth Largest Sum in a Binary Tree

Medium

You are given the root of a binary tree and a positive integer k.

The level sum in the tree is the sum of the values of the nodes that are on the same level.

Return the kth largest level sum in the tree (not necessarily distinct). If there are fewer than k levels in the tree, return -1.

Note that two nodes are on the same level if they have the same distance from the root.

 

Example 1:

Input: root = [5,8,9,2,1,3,7,4,6], k = 2
Output: 13
Explanation: The level sums are the following:
- Level 1: 5.
- Level 2: 8 + 9 = 17.
- Level 3: 2 + 1 + 3 + 7 = 13.
- Level 4: 4 + 6 = 10.
The 2nd largest level sum is 13.

Example 2:

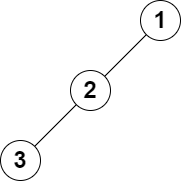
Input: root = [1,2,null,3], k = 1
Output: 3
Explanation: The largest level sum is 3.

 

Constraints:

• The number of nodes in the tree is n.
• 2 <= n <= 105
• 1 <= Node.val <= 106
• 1 <= k <= n

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public int val;
 *     public TreeNode left;
 *     public TreeNode right;
 *     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    public long KthLargestLevelSum(TreeNode root, int k)
    {
        //Step 1: push the sums to a hashtable, indexed by level
        Hashtable htSumByLevel = new Hashtable();
        CalculateLevelSum(root, 1, htSumByLevel);

        //Step 2: push all the values to a PQueue
        PriorityQueue pQueue = new PriorityQueue(false);
        foreach (int level in htSumByLevel.Keys) pQueue.Enqueue((long)htSumByLevel[level], (long)htSumByLevel[level]);

        //Step 3: dequeue until k
        long retVal = -1;
        while (k > 0)
        {
            if (pQueue.Count <= 0)
            {
                retVal = -1;
                break;
            }
            double temp = 0;
            retVal = (long)pQueue.Dequeue(out temp);
            k--;
        }

        return retVal;

    }

    private void CalculateLevelSum(TreeNode node, int level, Hashtable htSumByLevel)
    {
        if (node == null) return;
        if (!htSumByLevel.ContainsKey(level)) htSumByLevel.Add(level, 0L);
        htSumByLevel[level] = (long)htSumByLevel[level] + node.val;
        CalculateLevelSum(node.left, level + 1, htSumByLevel);
        CalculateLevelSum(node.right, level + 1, htSumByLevel);
    }
}

public class PriorityQueue
{
    public struct HeapEntry
    {
        private object item;
        private double priority;
        public HeapEntry(object item, double priority)
        {
            this.item = item;
            this.priority = priority;
        }
        public object Item
        {
            get
            {
                return item;
            }
        }
        public double Priority
        {
            get
            {
                return priority;
            }
        }
    }

    private bool ascend;
    private int count;
    private int capacity;
    private HeapEntry[] heap;

    public int Count
    {
        get
        {
            return this.count;
        }
    }

    public PriorityQueue(bool ascend, int cap = -1)
    {
        capacity = 10000000;
        if (cap > 0) capacity = cap;
        heap = new HeapEntry[capacity];
        this.ascend = ascend;
    }

    public object Dequeue(out double priority)
    {
        priority = heap[0].Priority;
        object result = heap[0].Item;
        count--;
        trickleDown(0, heap[count]);
        return result;
    }
    public object Peak(out double priority)
    {
        priority = heap[0].Priority;
        object result = heap[0].Item;
        return result;
    }

    public object Peak(/*out double priority*/)
    {
        //priority = heap[0].Priority;
        object result = heap[0].Item;
        return result;
    }

    public void Enqueue(object item, double priority)
    {
        count++;
        bubbleUp(count - 1, new HeapEntry(item, priority));
    }

    private void bubbleUp(int index, HeapEntry he)
    {
        int parent = (index - 1) / 2;
        // note: (index > 0) means there is a parent
        if (this.ascend)
        {
            while ((index > 0) && (heap[parent].Priority > he.Priority))
            {
                heap[index] = heap[parent];
                index = parent;
                parent = (index - 1) / 2;
            }
            heap[index] = he;
        }
        else
        {
            while ((index > 0) && (heap[parent].Priority < he.Priority))
            {
                heap[index] = heap[parent];
                index = parent;
                parent = (index - 1) / 2;
            }
            heap[index] = he;
        }
    }

    private void trickleDown(int index, HeapEntry he)
    {
        int child = (index * 2) + 1;
        while (child < count)
        {
            if (this.ascend)
            {
                if (((child + 1) < count) &&
                    (heap[child].Priority > heap[child + 1].Priority))
                {
                    child++;
                }
            }
            else
            {
                if (((child + 1) < count) &&
                    (heap[child].Priority < heap[child + 1].Priority))
                {
                    child++;
                }
            }
            heap[index] = heap[child];
            index = child;
            child = (index * 2) + 1;
        }
        bubbleUp(index, he);
    }
}