Cousins in a Binary Tree

Interesting problem about cousins in a binary tree. Cousins as the name implies are all the nodes in the same level that have different parent nodes.

Idea here is two-fold:

1/ First, perform a DFS and calculate the sum of all values per level. Use a Hashtable. This is done in linear time.

2/ Then, perform another DFS (also linear time) this time setting the values of the children. Do some calculation to get the sum of the siblings, and using the Hashtable calculated in #1, set the proper value for each child node

Code is down below, cheers, ACC.

Cousins in Binary Tree II - LeetCode

2641. Cousins in Binary Tree II

Medium

Given the root of a binary tree, replace the value of each node in the tree with the sum of all its cousins' values.

Two nodes of a binary tree are cousins if they have the same depth with different parents.

Return the root of the modified tree.

Note that the depth of a node is the number of edges in the path from the root node to it.

 

Example 1:

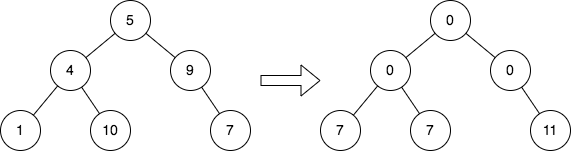
Input: root = [5,4,9,1,10,null,7]
Output: [0,0,0,7,7,null,11]
Explanation: The diagram above shows the initial binary tree and the binary tree after changing the value of each node.
- Node with value 5 does not have any cousins so its sum is 0.
- Node with value 4 does not have any cousins so its sum is 0.
- Node with value 9 does not have any cousins so its sum is 0.
- Node with value 1 has a cousin with value 7 so its sum is 7.
- Node with value 10 has a cousin with value 7 so its sum is 7.
- Node with value 7 has cousins with values 1 and 10 so its sum is 11.

Example 2:

Input: root = [3,1,2]
Output: [0,0,0]
Explanation: The diagram above shows the initial binary tree and the binary tree after changing the value of each node.
- Node with value 3 does not have any cousins so its sum is 0.
- Node with value 1 does not have any cousins so its sum is 0.
- Node with value 2 does not have any cousins so its sum is 0.

 

Constraints:

• The number of nodes in the tree is in the range [1, 105].
• 1 <= Node.val <= 104

Accepted

4,717

Submissions

7,943

public TreeNode ReplaceValueInTree(TreeNode root)
{
    Hashtable sumPerLevel = new Hashtable();
    SumValuesPerLevel(root, 0, sumPerLevel);

    root.val = 0;
    SetValuesOfChildren(root, 0, sumPerLevel);

    return root;
}

private void SetValuesOfChildren(TreeNode node,
                                    int level,
                                    Hashtable sumPerLevel)
{
    if (node == null || (node.left == null && node.right == null)) return;

    int sumChildren = (node.left != null ? node.left.val : 0) + (node.right != null ? node.right.val : 0);
    int sumLevel = (int)sumPerLevel[level + 1];

    if (node.left != null)
    {
        node.left.val = sumLevel - sumChildren;
        SetValuesOfChildren(node.left, level + 1, sumPerLevel);
    }
    if (node.right != null)
    {
        node.right.val = sumLevel - sumChildren;
        SetValuesOfChildren(node.right, level + 1, sumPerLevel);
    }
}

private void SumValuesPerLevel(TreeNode node,
                                int level,
                                Hashtable sumPerLevel)
{
    if (node == null) return;

    if (!sumPerLevel.ContainsKey(level)) sumPerLevel.Add(level, 0);
    sumPerLevel[level] = (int)sumPerLevel[level] + node.val;

    SumValuesPerLevel(node.left, level + 1, sumPerLevel);
    SumValuesPerLevel(node.right, level + 1, sumPerLevel);
}