Geometric Algorithms III

I tried this problem before but was actually over-complicating it a lot. Problem is simpler than I originally thought. Simply use the standard equation for a line, y=ax+b. Find (a,b) given the two first points. Then for every other point, check whether (y_point - a*x_point - b) is zero. That check needs to be a statistical one since we're dealing with floating points. Also take care of the special case where the line is of the form x=constant. Code is down below, cheers, ACC.

Check If It Is a Straight Line - LeetCode

1232. Check If It Is a Straight Line

Easy

You are given an array coordinates, coordinates[i] = [x, y], where [x, y] represents the coordinate of a point. Check if these points make a straight line in the XY plane.

 

 

Example 1:

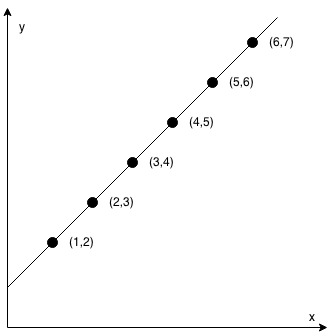
Input: coordinates = [[1,2],[2,3],[3,4],[4,5],[5,6],[6,7]]
Output: true

Example 2:

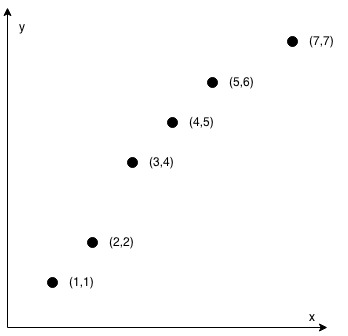
Input: coordinates = [[1,1],[2,2],[3,4],[4,5],[5,6],[7,7]]
Output: false

 

Constraints:

• 2 <= coordinates.length <= 1000
• coordinates[i].length == 2
• -10^4 <= coordinates[i][0], coordinates[i][1] <= 10^4
• coordinates contains no duplicate point.

Accepted

237,496

Submissions

595,091

public bool CheckStraightLine(int[][] coordinates)
{
    if (coordinates[1][0] != coordinates[0][0])
    {
        double a = (coordinates[1][1] - coordinates[0][1]) / (1.0 * (coordinates[1][0] - coordinates[0][0]));
        double b = coordinates[1][1] - a * coordinates[1][0];

        for (int i = 2; i < coordinates.Length; i++)
        {
            double err = coordinates[i][1] - a * coordinates[i][0] - b;
            if (!IsZero(err)) return false;
        }
        return true;
    }
    else
    {
        for (int i = 2; i < coordinates.Length; i++)
            if (coordinates[i][0] != coordinates[0][0]) return false;
        return true;
    }
}

private bool IsZero(double x)
{
    return Math.Abs(x) <= 0.000001;
}