Don't be ashamed of N^2 II

Medium-level problem but given the small constraints it becomes actually easy with an N^2 approach (N=2000). Find all the substrings and in the process use a mapping to calculate the sum, then check the sum%length condition. Code is down below, cheers, ACC.

Number of Divisible Substrings - LeetCode

2950. Number of Divisible Substrings

Medium

Each character of the English alphabet has been mapped to a digit as shown below.

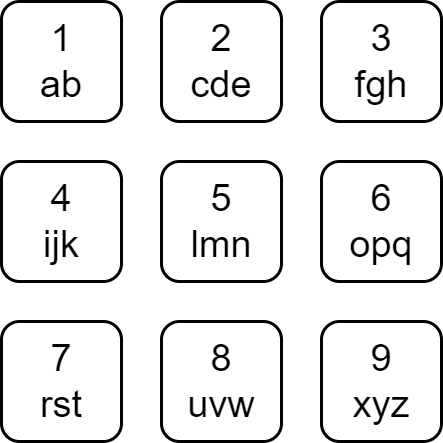
A string is divisible if the sum of the mapped values of its characters is divisible by its length.

Given a string s, return the number of divisible substrings of s.

A substring is a contiguous non-empty sequence of characters within a string.

 

Example 1:

Substring	Mapped	Sum	Length	Divisible?
a	1	1	1	Yes
s	7	7	1	Yes
d	2	2	1	Yes
f	3	3	1	Yes
as	1, 7	8	2	Yes
sd	7, 2	9	2	No
df	2, 3	5	2	No
asd	1, 7, 2	10	3	No
sdf	7, 2, 3	12	3	Yes
asdf	1, 7, 2, 3	13	4	No

Input: word = "asdf"
Output: 6
Explanation: The table above contains the details about every substring of word, and we can see that 6 of them are divisible.

Example 2:

Input: word = "bdh"
Output: 4
Explanation: The 4 divisible substrings are: "b", "d", "h", "bdh".
It can be shown that there are no other substrings of word that are divisible.

Example 3:

Input: word = "abcd"
Output: 6
Explanation: The 6 divisible substrings are: "a", "b", "c", "d", "ab", "cd".
It can be shown that there are no other substrings of word that are divisible.

 

Constraints:

• 1 <= word.length <= 2000
• word consists only of lowercase English letters.

public int CountDivisibleSubstrings(string word)
{
    int[] mapping = { 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5, 6, 6, 6, 7, 7, 7, 8, 8, 8, 9, 9, 9 };

    int retVal = 0;
    for (int i = 0; i < word.Length; i++)
    {
        int sum = 0;
        for (int j = i; j < word.Length; j++)
        {
            sum += mapping[(int)(word[j] - 'a')];
            if (sum % (j - i + 1) == 0) retVal++;
        }
    }

    return retVal;
}