Miller-Rabin Primality Test and Caching
Miller-Rabin remains one of the best practical primality testing available, despite the famous Primes is in P from 2003. Miller-Rabin is also a polynomial time algorithm but it is non-deterministic. However, given enough "iterations and witnesses", the non-deterministic aspect is so small that for all practical purposes it becomes deterministic. The implementation below for example has a probability of producing a wrong primality test of 9 x 10 ^ (-58) percent. The problem doesn't really need Miller-Rabin since the numbers are small but it is a good example of how to use it (together with some caching) to solve problems involving prime numbers in a very fast fashion. Code is down below, cheers, ACC.
Most Frequent Prime - LeetCode
You are given a m x n 0-indexed 2D matrix mat. From every cell, you can create numbers in the following way:
- There could be at most
8paths from the cells namely: east, south-east, south, south-west, west, north-west, north, and north-east. - Select a path from them and append digits in this path to the number being formed by traveling in this direction.
- Note that numbers are generated at every step, for example, if the digits along the path are
1, 9, 1, then there will be three numbers generated along the way:1, 19, 191.
Return the most frequent prime number greater than 10 out of all the numbers created by traversing the matrix or -1 if no such prime number exists. If there are multiple prime numbers with the highest frequency, then return the largest among them.
Note: It is invalid to change the direction during the move.
Example 1:
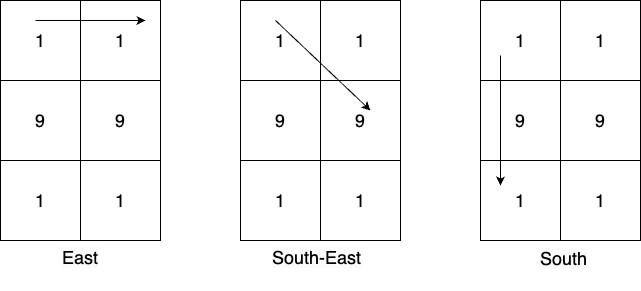
Input: mat = [[1,1],[9,9],[1,1]] Output: 19 Explanation: From cell (0,0) there are 3 possible directions and the numbers greater than 10 which can be created in those directions are: East: [11], South-East: [19], South: [19,191]. Numbers greater than 10 created from the cell (0,1) in all possible directions are: [19,191,19,11]. Numbers greater than 10 created from the cell (1,0) in all possible directions are: [99,91,91,91,91]. Numbers greater than 10 created from the cell (1,1) in all possible directions are: [91,91,99,91,91]. Numbers greater than 10 created from the cell (2,0) in all possible directions are: [11,19,191,19]. Numbers greater than 10 created from the cell (2,1) in all possible directions are: [11,19,19,191]. The most frequent prime number among all the created numbers is 19.
Example 2:
Input: mat = [[7]] Output: -1 Explanation: The only number which can be formed is 7. It is a prime number however it is not greater than 10, so return -1.
Example 3:
Input: mat = [[9,7,8],[4,6,5],[2,8,6]] Output: 97 Explanation: Numbers greater than 10 created from the cell (0,0) in all possible directions are: [97,978,96,966,94,942]. Numbers greater than 10 created from the cell (0,1) in all possible directions are: [78,75,76,768,74,79]. Numbers greater than 10 created from the cell (0,2) in all possible directions are: [85,856,86,862,87,879]. Numbers greater than 10 created from the cell (1,0) in all possible directions are: [46,465,48,42,49,47]. Numbers greater than 10 created from the cell (1,1) in all possible directions are: [65,66,68,62,64,69,67,68]. Numbers greater than 10 created from the cell (1,2) in all possible directions are: [56,58,56,564,57,58]. Numbers greater than 10 created from the cell (2,0) in all possible directions are: [28,286,24,249,26,268]. Numbers greater than 10 created from the cell (2,1) in all possible directions are: [86,82,84,86,867,85]. Numbers greater than 10 created from the cell (2,2) in all possible directions are: [68,682,66,669,65,658]. The most frequent prime number among all the created numbers is 97.
Constraints:
m == mat.lengthn == mat[i].length1 <= m, n <= 61 <= mat[i][j] <= 9
public class Solution {
public static Hashtable notPrime = new Hashtable();
public static Hashtable primesSet = new Hashtable();
public bool IsPrimeMillerRabin(BigInteger n)
{
if(primesSet.ContainsKey(n)) return true;
//It does not work well for smaller numbers, hence this check
int SMALL_NUMBER = 1000;
if (n <= SMALL_NUMBER)
{
return IsPrime(n);
}
int MAX_WITNESS = 100;
for (long i = 2; i <= MAX_WITNESS; i++)
{
if (IsPrime(i) && Witness(i, n) == 1)
{
return false;
}
}
if(!primesSet.ContainsKey(n)) primesSet.Add(n, true);
return true;
}
public BigInteger SqRtN(BigInteger N)
{
/*++
* Using Newton Raphson method we calculate the
* square root (N/g + g)/2
*/
BigInteger rootN = N;
int count = 0;
int bitLength = 1;
while (rootN / 2 != 0)
{
rootN /= 2;
bitLength++;
}
bitLength = (bitLength + 1) / 2;
rootN = N >> bitLength;
BigInteger lastRoot = BigInteger.Zero;
do
{
if (lastRoot > rootN)
{
if (count++ > 1000) // Work around for the bug where it gets into an infinite loop
{
return rootN;
}
}
lastRoot = rootN;
rootN = (BigInteger.Divide(N, rootN) + rootN) >> 1;
}
while (!((rootN ^ lastRoot).ToString() == "0"));
return rootN;
}
public bool IsPrime(BigInteger n)
{
if (n <= 1)
{
return false;
}
if (n == 2)
{
return true;
}
if (n % 2 == 0)
{
return false;
}
for (int i = 3; i <= SqRtN(n) + 1; i += 2)
{
if (n % i == 0)
{
return false;
}
}
return true;
}
private int Witness(long a, BigInteger n)
{
BigInteger t, u;
BigInteger prev, curr = 0;
BigInteger i;
BigInteger lln = n;
u = n / 2;
t = 1;
while (u % 2 == 0)
{
u /= 2;
t++;
}
prev = BigInteger.ModPow(a, u, n);
for (i = 1; i <= t; i++)
{
curr = BigInteger.ModPow(prev, 2, lln);
if ((curr == 1) && (prev != 1) && (prev != lln - 1)) return 1;
prev = curr;
}
if (curr != 1) return 1;
return 0;
}
public int MostFrequentPrime(int[][] mat)
{
Hashtable primeFrequency = new Hashtable();
int maxFrequency = 0;
int maxPrime = -1;
for (int r = 0; r < mat.Length; r++)
{
for (int c = 0; c < mat[r].Length; c++)
{
CalculateAllPrimesFromPosition(mat, r, c, primeFrequency, ref maxFrequency, ref maxPrime);
}
}
return maxPrime;
}
private void CalculateAllPrimesFromPosition(int[][] mat,
int row,
int col,
Hashtable primeFrequency,
ref int maxFrequency,
ref int maxPrime)
{
int number = 0;
int r = 0;
int c = 0;
number = 0;
for (int i = row; i < mat.Length; i++)
{
number = 10 * number + mat[i][col];
if (number > 10)
{
if (primeFrequency.ContainsKey(number)) primeFrequency[number] = (int)primeFrequency[number] + 1;
else if (!notPrime.ContainsKey(number))
{
if (IsPrimeMillerRabin(number)) primeFrequency.Add(number, 1);
else notPrime.Add(number, true);
}
if (primeFrequency.ContainsKey(number))
{
if ((int)primeFrequency[number] > maxFrequency)
{
maxFrequency = (int)primeFrequency[number];
maxPrime = number;
}
else if ((int)primeFrequency[number] == maxFrequency)
{
maxPrime = Math.Max(maxPrime, number);
}
}
}
}
number = 0;
for (int i = col; i < mat[0].Length; i++)
{
number = 10 * number + mat[row][i];
if (number > 10)
{
if (primeFrequency.ContainsKey(number)) primeFrequency[number] = (int)primeFrequency[number] + 1;
else if (!notPrime.ContainsKey(number))
{
if (IsPrimeMillerRabin(number)) primeFrequency.Add(number, 1);
else notPrime.Add(number, true);
}
if (primeFrequency.ContainsKey(number))
{
if ((int)primeFrequency[number] > maxFrequency)
{
maxFrequency = (int)primeFrequency[number];
maxPrime = number;
}
else if ((int)primeFrequency[number] == maxFrequency)
{
maxPrime = Math.Max(maxPrime, number);
}
}
}
}
number = 0;
for (int i = row; i >= 0; i--)
{
number = 10 * number + mat[i][col];
if (number > 10)
{
if (primeFrequency.ContainsKey(number)) primeFrequency[number] = (int)primeFrequency[number] + 1;
else if (!notPrime.ContainsKey(number))
{
if (IsPrimeMillerRabin(number)) primeFrequency.Add(number, 1);
else notPrime.Add(number, true);
}
if (primeFrequency.ContainsKey(number))
{
if ((int)primeFrequency[number] > maxFrequency)
{
maxFrequency = (int)primeFrequency[number];
maxPrime = number;
}
else if ((int)primeFrequency[number] == maxFrequency)
{
maxPrime = Math.Max(maxPrime, number);
}
}
}
}
number = 0;
for (int i = col; i >= 0; i--)
{
number = 10 * number + mat[row][i];
if (number > 10)
{
if (primeFrequency.ContainsKey(number)) primeFrequency[number] = (int)primeFrequency[number] + 1;
else if (!notPrime.ContainsKey(number))
{
if (IsPrimeMillerRabin(number)) primeFrequency.Add(number, 1);
else notPrime.Add(number, true);
}
if (primeFrequency.ContainsKey(number))
{
if ((int)primeFrequency[number] > maxFrequency)
{
maxFrequency = (int)primeFrequency[number];
maxPrime = number;
}
else if ((int)primeFrequency[number] == maxFrequency)
{
maxPrime = Math.Max(maxPrime, number);
}
}
}
}
number = 0;
r = row;
c = col;
while (r >= 0 && r < mat.Length && c >= 0 && c < mat[r].Length)
{
number = 10 * number + mat[r][c];
if (number > 10)
{
if (primeFrequency.ContainsKey(number)) primeFrequency[number] = (int)primeFrequency[number] + 1;
else if (!notPrime.ContainsKey(number))
{
if (IsPrimeMillerRabin(number)) primeFrequency.Add(number, 1);
else notPrime.Add(number, true);
}
if (primeFrequency.ContainsKey(number))
{
if ((int)primeFrequency[number] > maxFrequency)
{
maxFrequency = (int)primeFrequency[number];
maxPrime = number;
}
else if ((int)primeFrequency[number] == maxFrequency)
{
maxPrime = Math.Max(maxPrime, number);
}
}
}
r++;
c++;
}
number = 0;
r = row;
c = col;
while (r >= 0 && r < mat.Length && c >= 0 && c < mat[r].Length)
{
number = 10 * number + mat[r][c];
if (number > 10)
{
if (primeFrequency.ContainsKey(number)) primeFrequency[number] = (int)primeFrequency[number] + 1;
else if (!notPrime.ContainsKey(number))
{
if (IsPrimeMillerRabin(number)) primeFrequency.Add(number, 1);
else notPrime.Add(number, true);
}
if (primeFrequency.ContainsKey(number))
{
if ((int)primeFrequency[number] > maxFrequency)
{
maxFrequency = (int)primeFrequency[number];
maxPrime = number;
}
else if ((int)primeFrequency[number] == maxFrequency)
{
maxPrime = Math.Max(maxPrime, number);
}
}
}
r++;
c--;
}
number = 0;
r = row;
c = col;
while (r >= 0 && r < mat.Length && c >= 0 && c < mat[r].Length)
{
number = 10 * number + mat[r][c];
if (number > 10)
{
if (primeFrequency.ContainsKey(number)) primeFrequency[number] = (int)primeFrequency[number] + 1;
else if (!notPrime.ContainsKey(number))
{
if (IsPrimeMillerRabin(number)) primeFrequency.Add(number, 1);
else notPrime.Add(number, true);
}
if (primeFrequency.ContainsKey(number))
{
if ((int)primeFrequency[number] > maxFrequency)
{
maxFrequency = (int)primeFrequency[number];
maxPrime = number;
}
else if ((int)primeFrequency[number] == maxFrequency)
{
maxPrime = Math.Max(maxPrime, number);
}
}
}
r--;
c++;
}
number = 0;
r = row;
c = col;
while (r >= 0 && r < mat.Length && c >= 0 && c < mat[r].Length)
{
number = 10 * number + mat[r][c];
if (number > 10)
{
if (primeFrequency.ContainsKey(number)) primeFrequency[number] = (int)primeFrequency[number] + 1;
else if (!notPrime.ContainsKey(number))
{
if (IsPrimeMillerRabin(number)) primeFrequency.Add(number, 1);
else notPrime.Add(number, true);
}
if (primeFrequency.ContainsKey(number))
{
if ((int)primeFrequency[number] > maxFrequency)
{
maxFrequency = (int)primeFrequency[number];
maxPrime = number;
}
else if ((int)primeFrequency[number] == maxFrequency)
{
maxPrime = Math.Max(maxPrime, number);
}
}
}
r--;
c--;
}
}
}



Comments
Post a Comment