Standard Priority Queue V: PQueue as a Sorting Mechanism

Priority Queues can be used as a standard NLogN sorting mechanism. Usually it isn't used as sorting due to the extra space required for the heap, but in terms of execution time it is as efficient as MergeSort for the worst case and even better than QuickSort on some cases. If you have a handy implementation of PQueue, don't be afraid of using it for sorting.

Problem below requires a sorting of the elements based on the X-coordinate, followed by a linear scanning counting the number of rectangles. PQueue comes to the rescue here. Code is down below, cheers, ACC.

Minimum Rectangles to Cover Points - LeetCode

3111. Minimum Rectangles to Cover Points

Medium

You are given a 2D integer array points, where points[i] = [xi, yi]. You are also given an integer w. Your task is to cover all the given points with rectangles.

Each rectangle has its lower end at some point (x1, 0) and its upper end at some point (x2, y2), where x1 <= x2, y2 >= 0, and the condition x2 - x1 <= w must be satisfied for each rectangle.

A point is considered covered by a rectangle if it lies within or on the boundary of the rectangle.

Return an integer denoting the minimum number of rectangles needed so that each point is covered by at least one rectangle.

Note: A point may be covered by more than one rectangle.

 

Example 1:

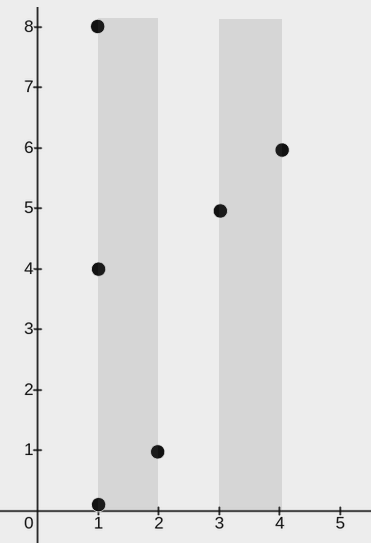
Input: points = [[2,1],[1,0],[1,4],[1,8],[3,5],[4,6]], w = 1

Output: 2

Explanation:

The image above shows one possible placement of rectangles to cover the points:

• A rectangle with a lower end at (1, 0) and its upper end at (2, 8)
• A rectangle with a lower end at (3, 0) and its upper end at (4, 8)

Example 2:

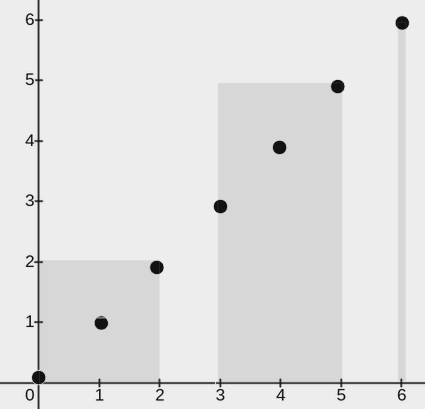
Input: points = [[0,0],[1,1],[2,2],[3,3],[4,4],[5,5],[6,6]], w = 2

Output: 3

Explanation:

The image above shows one possible placement of rectangles to cover the points:

• A rectangle with a lower end at (0, 0) and its upper end at (2, 2)
• A rectangle with a lower end at (3, 0) and its upper end at (5, 5)
• A rectangle with a lower end at (6, 0) and its upper end at (6, 6)

Example 3:

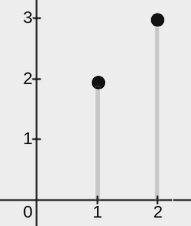
Input: points = [[2,3],[1,2]], w = 0

Output: 2

Explanation:

The image above shows one possible placement of rectangles to cover the points:

• A rectangle with a lower end at (1, 0) and its upper end at (1, 2)
• A rectangle with a lower end at (2, 0) and its upper end at (2, 3)

 

Constraints:

• 1 <= points.length <= 105
• points[i].length == 2
• 0 <= xi == points[i][0] <= 109
• 0 <= yi == points[i][1] <= 109
• 0 <= w <= 109
• All pairs (xi, yi) are distinct.

public class Solution {
    public int MinRectanglesToCoverPoints(int[][] points, int w)
    {
        PriorityQueue pQueue = new PriorityQueue(true, 100000 + 7);

        foreach (int[] point in points)
            pQueue.Enqueue(point, point[0]);

        bool initBlock = true;
        int initX = 0;
        int retVal = 0;

        while (pQueue.Count > 0)
        {
            double x = 0;
            int[] point = (int[])pQueue.Dequeue(out x);

            if (initBlock)
            {
                initX = point[0];
                initBlock = false;
                retVal++;
            }
            else if (point[0] - initX > w)
            {
                initX = point[0];
                retVal++;
            }
        }

        return retVal;
    }
}

public class PriorityQueue
{
    public struct HeapEntry
    {
        private object item;
        private double priority;
        public HeapEntry(object item, double priority)
        {
            this.item = item;
            this.priority = priority;
        }
        public object Item
        {
            get
            {
                return item;
            }
        }
        public double Priority
        {
            get
            {
                return priority;
            }
        }
    }

    private bool ascend;
    private int count;
    private int capacity;
    private HeapEntry[] heap;

    public int Count
    {
        get
        {
            return this.count;
        }
    }

    public PriorityQueue(bool ascend, int cap = -1)
    {
        capacity = 10000000;
        if (cap > 0) capacity = cap;
        heap = new HeapEntry[capacity];
        this.ascend = ascend;
    }

    public object Dequeue(out double priority)
    {
        priority = heap[0].Priority;
        object result = heap[0].Item;
        count--;
        trickleDown(0, heap[count]);
        return result;
    }
    public object Peak(out double priority)
    {
        priority = heap[0].Priority;
        object result = heap[0].Item;
        return result;
    }

    public object Peak(/*out double priority*/)
    {
        //priority = heap[0].Priority;
        object result = heap[0].Item;
        return result;
    }

    public void Enqueue(object item, double priority)
    {
        count++;
        bubbleUp(count - 1, new HeapEntry(item, priority));
    }

    private void bubbleUp(int index, HeapEntry he)
    {
        int parent = (index - 1) / 2;
        // note: (index > 0) means there is a parent
        if (this.ascend)
        {
            while ((index > 0) && (heap[parent].Priority > he.Priority))
            {
                heap[index] = heap[parent];
                index = parent;
                parent = (index - 1) / 2;
            }
            heap[index] = he;
        }
        else
        {
            while ((index > 0) && (heap[parent].Priority < he.Priority))
            {
                heap[index] = heap[parent];
                index = parent;
                parent = (index - 1) / 2;
            }
            heap[index] = he;
        }
    }

    private void trickleDown(int index, HeapEntry he)
    {
        int child = (index * 2) + 1;
        while (child < count)
        {
            if (this.ascend)
            {
                if (((child + 1) < count) &&
                    (heap[child].Priority > heap[child + 1].Priority))
                {
                    child++;
                }
            }
            else
            {
                if (((child + 1) < count) &&
                    (heap[child].Priority < heap[child + 1].Priority))
                {
                    child++;
                }
            }
            heap[index] = heap[child];
            index = child;
            child = (index * 2) + 1;
        }
        bubbleUp(index, he);
    }
}