Grid - Breadth First Search (BFS) - IV

Requires a standard BFS to solve it. The only caveat is that you may reach a cell that has been reached before but if you reach it with more health than before, it is OK to proceed. Code is down below, cheers, ACC.

Find a Safe Walk Through a Grid - LeetCode

3286. Find a Safe Walk Through a Grid

Medium

You are given an m x n binary matrix grid and an integer health.

You start on the upper-left corner (0, 0) and would like to get to the lower-right corner (m - 1, n - 1).

You can move up, down, left, or right from one cell to another adjacent cell as long as your health remains positive.

Cells (i, j) with grid[i][j] = 1 are considered unsafe and reduce your health by 1.

Return true if you can reach the final cell with a health value of 1 or more, and false otherwise.

 

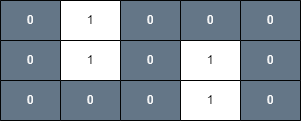
Example 1:

Input: grid = [[0,1,0,0,0],[0,1,0,1,0],[0,0,0,1,0]], health = 1

Output: true

Explanation:

The final cell can be reached safely by walking along the gray cells below.

Example 2:

Input: grid = [[0,1,1,0,0,0],[1,0,1,0,0,0],[0,1,1,1,0,1],[0,0,1,0,1,0]], health = 3

Output: false

Explanation:

A minimum of 4 health points is needed to reach the final cell safely.

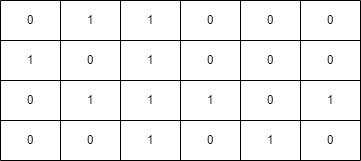
Example 3:

Input: grid = [[1,1,1],[1,0,1],[1,1,1]], health = 5

Output: true

Explanation:

The final cell can be reached safely by walking along the gray cells below.

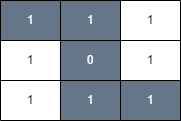
Any path that does not go through the cell (1, 1) is unsafe since your health will drop to 0 when reaching the final cell.

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 50
• 2 <= m * n
• 1 <= health <= m + n
• grid[i][j] is either 0 or 1.

Accepted

17,352

Submissions

68,289

public class CellHealth
{
    public int row = 0;
    public int col = 0;
    public int health = 0;
    public int key = 0;

    public CellHealth(int row, int col, int health)
    {
        this.row = row;
        this.col = col;
        this.health = health;

        this.key = row * 57 + col;
    }
}

public bool FindSafeWalk(IList> grid, int health)
{
    Queue queue = new Queue();
    CellHealth cellHealth = new CellHealth(0, 0, (grid[0][0] == 1) ? health - 1 : health);
    queue.Enqueue(cellHealth);

    Hashtable visited = new Hashtable();
    visited.Add(cellHealth.key, cellHealth.health);

    while (queue.Count > 0)
    {
        CellHealth currentCellHealth = queue.Dequeue();

        if (currentCellHealth.row == grid.Count - 1 &&
            currentCellHealth.col == grid[grid.Count - 1].Count - 1 &&
            currentCellHealth.health > 0)
        {
            return true;
        }

        int[] deltaRow = { 1, -1, 0, 0 };
        int[] deltaCol = { 0, 0, 1, -1 };

        for (int i = 0; i < deltaRow.Length; i++)
        {
            int newRow = currentCellHealth.row + deltaRow[i];
            int newCol = currentCellHealth.col + deltaCol[i];

            if (newRow >= 0 &&
                newRow < grid.Count &&
                newCol >= 0 &&
                newCol < grid[newRow].Count)
            {
                CellHealth newCellHealth = new CellHealth(newRow, newCol, (grid[newRow][newCol] == 1) ? currentCellHealth.health - 1 : currentCellHealth.health);
                if (newCellHealth.health > 0)
                {
                    if (!visited.ContainsKey(newCellHealth.key))
                    {
                        queue.Enqueue(newCellHealth);
                        visited.Add(newCellHealth.key, newCellHealth.health);
                    }
                    else
                    {
                        int vHealth = (int)visited[newCellHealth.key];
                        if (vHealth < newCellHealth.health)
                        {
                            queue.Enqueue(newCellHealth);
                            visited[newCellHealth.key] = newCellHealth.health;
                        }
                    }
                }
            }
        }
    }

    return false;
}