Diagonals

We need to sort the diagonals of a matrix. The approach that I use here is the following:

1. Create a Hashtable where the key is the diagonal index. The diagonal index is just the row-col

2. Traverse the matrix adding the elements as a list to the corresponding Hashtable entry

3. Traverse the Hashtable and sort each list (you need to store in a different Hashtable)

4. Traverse the matrix again. Now that you have the diagonal index, get the corresponding element using the Hashtable

5. Remove the corresponding element from the list, depending whether you're sorting up or down

Code is down below, cheers, ACC

Sort Matrix by Diagonals - LeetCode

You are given an n x n square matrix of integers grid. Return the matrix such that:

• The diagonals in the bottom-left triangle (including the middle diagonal) are sorted in non-increasing order.
• The diagonals in the top-right triangle are sorted in non-decreasing order.

 

Example 1:

Input: grid = [[1,7,3],[9,8,2],[4,5,6]]

Output: [[8,2,3],[9,6,7],[4,5,1]]

Explanation:

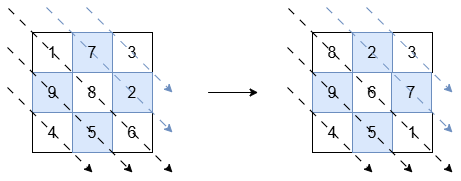
The diagonals with a black arrow (bottom-left triangle) should be sorted in non-increasing order:

• [1, 8, 6] becomes [8, 6, 1].
• [9, 5] and [4] remain unchanged.

The diagonals with a blue arrow (top-right triangle) should be sorted in non-decreasing order:

• [7, 2] becomes [2, 7].
• [3] remains unchanged.

Example 2:

Input: grid = [[0,1],[1,2]]

Output: [[2,1],[1,0]]

Explanation:

The diagonals with a black arrow must be non-increasing, so [0, 2] is changed to [2, 0]. The other diagonals are already in the correct order.

Example 3:

Input: grid = [[1]]

Output: [[1]]

Explanation:

Diagonals with exactly one element are already in order, so no changes are needed.

 

Constraints:

• grid.length == grid[i].length == n
• 1 <= n <= 10
• -105 <= grid[i][j] <= 105

public int[][] SortMatrix(int[][] grid)
{
    Hashtable diagonals = new Hashtable();

    for (int row = 0; row < grid.Length; row++)
    {
        for (int col = 0; col < grid[row].Length; col++)
        {
            int diagonalIndex = row - col;
            if (!diagonals.ContainsKey(diagonalIndex)) diagonals.Add(diagonalIndex, new List());
            List list = (List)diagonals[diagonalIndex];
            list.Add(grid[row][col]);
        }
    }

    Hashtable sortedDiagonals = new Hashtable();
    foreach (int diagonalIndex in diagonals.Keys)
    {
        List list = (List)diagonals[diagonalIndex];
        int[] arr = list.ToArray();
        Array.Sort(arr);
        sortedDiagonals.Add(diagonalIndex, arr.ToList());
    }

    int[][] retVal = new int[grid.Length][];
    for (int row = 0; row < grid.Length; row++)
    {
        retVal[row] = new int[grid[row].Length];
        for (int col = 0; col < grid[row].Length; col++)
        {
            int diagonalIndex = row - col;
            List list = (List)sortedDiagonals[diagonalIndex];
            if (diagonalIndex < 0)
            {
                retVal[row][col] = list[0];
                list.RemoveAt(0);
            }
            else
            {
                retVal[row][col] = list[list.Count - 1];
                list.RemoveAt(list.Count - 1);
            }
        }
    }

    return retVal;
}