LeetCode: Combination Sum III
https://leetcode.com/problems/combination-sum-iii/, here is the problem definition:
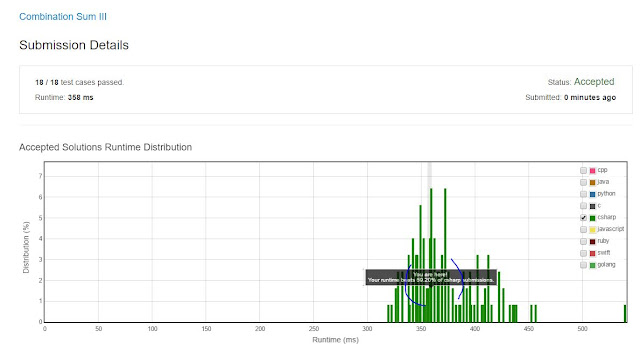
The solution is a DFS (Depth-First-Search), cutting down the combinations by trimming the search in the base case (no need to go further past k, or when the sum is past n). It is a standard base-case-induction-case algorithm. Some nuances of the language to be aware of: for instance the line in bold is necessary 'cause if you try to add "currentSet" to the solution it will be empty since it is being operated by reference rather than by value. The solution isn't that fast, only beating 60% of the c# submissions. There are problem further optimizations that can be done given the constraints (in addition to removing the stack-based recursion). Cheers, Marcelo.
public class Solution
{
public IList<IList<int>> CombinationSum3(int k, int n)
{
IList<IList<int>> solution = new List<IList<int>>();
CombinationSum3Internal(new List<int>(), 0, 1, k, n, solution);
return solution;
}
private void CombinationSum3Internal(List<int> currentSet,
int currentSum,
int currentIndex,
int k,
int n,
IList<IList<int>> solution)
{
//Base case
if (currentSet.Count >= k)
{
if (currentSum == n)
{
List<int> copySet = new List<int>(currentSet);
solution.Add(copySet);
}
return;
}
else if (currentSum >= n)
{
return;
}
//Induction
for (int i = currentIndex; i < 10; i++)
{
currentSet.Add(i);
CombinationSum3Internal(currentSet, currentSum + i, i + 1, k, n, solution);
currentSet.Remove(i);
}
}
}
Find all possible combinations of k numbers that add up to a number n, given that only numbers from 1 to 9 can be used and each combination should be a unique set of numbers.
Example 1:
Input: k = 3, n = 7
Output:
[[1,2,4]]
Example 2:
Input: k = 3, n = 9
Output:
[[1,2,6], [1,3,5], [2,3,4]]
The solution is a DFS (Depth-First-Search), cutting down the combinations by trimming the search in the base case (no need to go further past k, or when the sum is past n). It is a standard base-case-induction-case algorithm. Some nuances of the language to be aware of: for instance the line in bold is necessary 'cause if you try to add "currentSet" to the solution it will be empty since it is being operated by reference rather than by value. The solution isn't that fast, only beating 60% of the c# submissions. There are problem further optimizations that can be done given the constraints (in addition to removing the stack-based recursion). Cheers, Marcelo.
public class Solution
{
public IList<IList<int>> CombinationSum3(int k, int n)
{
IList<IList<int>> solution = new List<IList<int>>();
CombinationSum3Internal(new List<int>(), 0, 1, k, n, solution);
return solution;
}
private void CombinationSum3Internal(List<int> currentSet,
int currentSum,
int currentIndex,
int k,
int n,
IList<IList<int>> solution)
{
//Base case
if (currentSet.Count >= k)
{
if (currentSum == n)
{
List<int> copySet = new List<int>(currentSet);
solution.Add(copySet);
}
return;
}
else if (currentSum >= n)
{
return;
}
//Induction
for (int i = currentIndex; i < 10; i++)
{
currentSet.Add(i);
CombinationSum3Internal(currentSet, currentSum + i, i + 1, k, n, solution);
currentSet.Remove(i);
}
}
}



Very nice Marcelo! My solution is almost identical:
ReplyDeleteclass Solution {
private:
void helper(int start, int k, int n, vector &temp, vector> &res) {
if (k == 0 && n == 0) res.push_back(temp);
if (n < 0 || k == 0 || pow(10, k) < n) return;
for (int i = start; i < 10; ++i) {
if (i > n) break;
temp.push_back(i);
helper(i+1, k-1, n-i, temp, res);
temp.pop_back();
}
}
public:
vector> combinationSum3(int k, int n) {
vector> res;
vector temp; temp.reserve(k);
helper(1, k, n, temp, res);
return res;
}
};
Unfortunately since it takes only 0ms to run, my experiments with different branch pruning strategies were fruitless :(