200 problems solved on LeetCode
Howdy!!!
I had solved 203 problems on Project Euler, until it got hacked.
I had solved 200+ problems on Hacker-Rank, until I ran out of easy/medium problems to solve.
Now I've crossed the 200 problems mark on LeetCode. I think I can get to the 300 there, assuming they keep on posting easy/medium problems, and that my interest for TV shows continue to be zero.
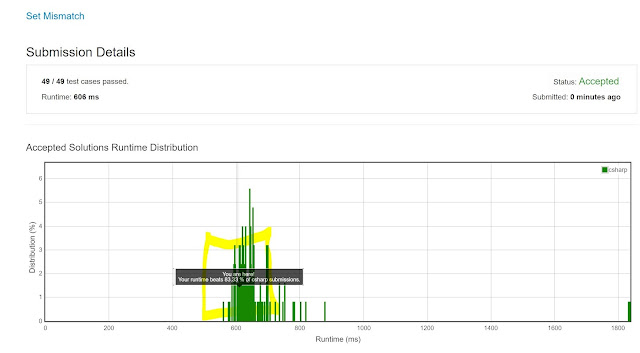
The 200th problem was this one: https://leetcode.com/problems/set-mismatch/description/:
The set
S originally contains numbers from 1 to n. But unfortunately, due to the data error, one of the numbers in the set got duplicated to another number in the set, which results in repetition of one number and loss of another number.
Given an array
nums representing the data status of this set after the error. Your task is to firstly find the number occurs twice and then find the number that is missing. Return them in the form of an array.
Example 1:
Input: nums = [1,2,2,4] Output: [2,3]
Note:
- The given array size will in the range [2, 10000].
- The given array's numbers won't have any order.
Relatively straightforward:
- Have a bucket from 0..N-1
- Assume it is zero'ed upon init
- Run the array once, increment the bucket item accordingly
- Run it again, catch the numbers you're looking for
O(n)-time, O(n)-space. Code is below. Many cheers, Marcelo.
public class Solution
{
public int[] FindErrorNums(int[] nums)
{
int[] buckets = new int[nums.Length];
for (int i = 0; i < nums.Length; i++)
{
buckets[nums[i] - 1]++;
}
int dupe = -1;
int miss = -1;
for (int i = 0;i < buckets.Length; i++)
{
if (buckets[i] == 0) miss = i + 1;
if (buckets[i] == 2) dupe = i + 1;
}
return new int[] { dupe, miss };
}
}



Wow, congratulations on such an awesome achievement! I don't know anyone else who solved more than 200 problems on Project Euler and while it may just mean that I don't know a lot of people, something tells me that the reason is different and you rock!
ReplyDeleteInterestingly for this particular problem, I decided to use a more analytical way of computing the answer - by playing a little with series sums it's possible to come up with a system of equations and solve it using only a constant space.
My solution with explanation in comments below:
class Solution {
public:
vector findErrorNums(const vector& nums) {
long n = nums.size();
long sum1 = n * (n + 1) / 2; // sum of 1..n
long sq_sum1 = n * (n + 1) * (2 * n + 1) / 6; // sum of 1^2 .. n^2
long sum2 = 0; // sum of 1 .. x .. y .. n
long sq_sum2 = 0; // sum of 1^2 .. x^2 .. y^2 .. n^2
for (long num : nums) {
sum2 += num;
sq_sum2 += num * num;
}
// x - y = sum2 - sum1
long diff12 = sum1 - sum2;
// y = x + diff12
// x^2 - y^2 = sq_sum2 - sq_sum1
// x^2 - (x^2 + 2*x*diff12 + diff12^2) = sq_sum2 - sq_sum1
// -2*x*diff12 = sq_sum2 - sq_sum1 + diff12^2
// x = -(sq_sum2 - sq_sum1 + diff12^2) / (2*diff12)
long x = (sq_sum1 - sq_sum2 - diff12*diff12) / (2*diff12);
long y = x + diff12;
return {x, y};
}
};
and in case anyone is interested in playing with code - https://ideone.com/qYToYh
Congrats again and I'm looking forward to the next 200 hundred problems!