Trees, Palindromes and C#

Great problem covering all three aspects - tree, palindromes and peculiarities of the C# language: https://leetcode.com/problems/pseudo-palindromic-paths-in-a-binary-tree/

1457. Pseudo-Palindromic Paths in a Binary Tree

Medium

Given a binary tree where node values are digits from 1 to 9. A path in the binary tree is said to be pseudo-palindromic if at least one permutation of the node values in the path is a palindrome.

Return the number of pseudo-palindromic paths going from the root node to leaf nodes.

 

Example 1:

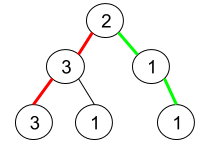
Input: root = [2,3,1,3,1,null,1]
Output: 2 
Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the red path [2,3,3], the green path [2,1,1], and the path [2,3,1]. Among these paths only red path and green path are pseudo-palindromic paths since the red path [2,3,3] can be rearranged in [3,2,3] (palindrome) and the green path [2,1,1] can be rearranged in [1,2,1] (palindrome).

Example 2:

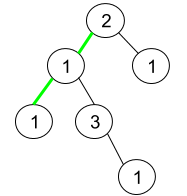
Input: root = [2,1,1,1,3,null,null,null,null,null,1]
Output: 1 
Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the green path [2,1,1], the path [2,1,3,1], and the path [2,1]. Among these paths only the green path is pseudo-palindromic since [2,1,1] can be rearranged in [1,2,1] (palindrome).

Example 3:

Input: root = [9]
Output: 1

 

Constraints:

• The given binary tree will have between 1 and 10^5 nodes.
• Node values are digits from 1 to 9.

Accepted

7,745

Submissions

11,802

Firs, for the palindrome, to check whether the permutation of a set of elements is a palindrome can be done in linear time with the "bucketization" technique: count the frequency of each character. As long as there is no more than one odd frequency, the set is palindromic. Traverse the tree using standard DFS. But keep in mind that in C# the objects are passed by reference, hemce you'll need to keep updating the buckets array as you pass it along. Cheers, ACC.

public class Solution

{

    public int PseudoPalindromicPaths(TreeNode root)

    {

        int[] buckets = new int[10];

        return PseudoPalindromicPaths(root, buckets);

    }

    private int PseudoPalindromicPaths(TreeNode node, int[] buckets)

    {

        if (node == null) return 0;

        if (node.left == null && node.right == null)

        {

            buckets[node.val - 1]++;

            int retVal = 0;

            if (IsPermutationPalindrome(buckets)) retVal = 1;

            buckets[node.val - 1]--;

            return retVal;

        }

        buckets[node.val - 1]++;

        int right = PseudoPalindromicPaths(node.right, buckets);

        int left = PseudoPalindromicPaths(node.left, buckets);

        buckets[node.val - 1]--;

        return right + left;

    }

    private bool IsPermutationPalindrome(int[] buckets)

    {

        int nOdds = 0;

        for (int i = 0; i < buckets.Length; i++)

        {

            if (buckets[i] % 2 == 1) nOdds++;

            if (nOdds > 1) return false;

        }

        return true;

    }

}