Grid - Breadth First Search (BFS) - III

LeetCode just loves to bring BFS problems. This one is very similar to the previous ones related to grids (in the case here it is a Maze, but the idea is the same). Nothing really different in this problem that is worth explaining further, so just enjoy the code down below - cheers, ACC.

Nearest Exit from Entrance in Maze - LeetCode

1926. Nearest Exit from Entrance in Maze

Medium

You are given an m x n matrix maze (0-indexed) with empty cells (represented as '.') and walls (represented as '+'). You are also given the entrance of the maze, where entrance = [entrancerow, entrancecol] denotes the row and column of the cell you are initially standing at.

In one step, you can move one cell up, down, left, or right. You cannot step into a cell with a wall, and you cannot step outside the maze. Your goal is to find the nearest exit from the entrance. An exit is defined as an empty cell that is at the border of the maze. The entrance does not count as an exit.

Return the number of steps in the shortest path from the entrance to the nearest exit, or -1 if no such path exists.

 

Example 1:

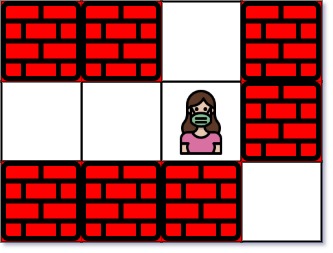
Input: maze = [["+","+",".","+"],[".",".",".","+"],["+","+","+","."]], entrance = [1,2]
Output: 1
Explanation: There are 3 exits in this maze at [1,0], [0,2], and [2,3].
Initially, you are at the entrance cell [1,2].
- You can reach [1,0] by moving 2 steps left.
- You can reach [0,2] by moving 1 step up.
It is impossible to reach [2,3] from the entrance.
Thus, the nearest exit is [0,2], which is 1 step away.

Example 2:

Input: maze = [["+","+","+"],[".",".","."],["+","+","+"]], entrance = [1,0]
Output: 2
Explanation: There is 1 exit in this maze at [1,2].
[1,0] does not count as an exit since it is the entrance cell.
Initially, you are at the entrance cell [1,0].
- You can reach [1,2] by moving 2 steps right.
Thus, the nearest exit is [1,2], which is 2 steps away.

Example 3:

Input: maze = [[".","+"]], entrance = [0,0]
Output: -1
Explanation: There are no exits in this maze.

 

Constraints:

• maze.length == m
• maze[i].length == n
• 1 <= m, n <= 100
• maze[i][j] is either '.' or '+'.
• entrance.length == 2
• 0 <= entrancerow < m
• 0 <= entrancecol < n
• entrance will always be an empty cell.

class MazeCell
{
    public int row = 0;
    public int col = 0;
    public int steps = 0;
    public int key = 0;
    public MazeCell(int row, int col, int steps)
    {
        this.row = row;
        this.col = col;
        this.steps = steps;

        key = 102 * row + col;
    }
}

public class Solution
{
    public int NearestExit(char[][] maze, int[] entrance)
    {
        Queue queue = new Queue();
        Hashtable visited = new Hashtable();

        MazeCell mazeCell = new MazeCell(entrance[0], entrance[1], 0);
        queue.Enqueue(mazeCell);
        visited.Add(mazeCell.key, true);

        while (queue.Count > 0)
        {
            MazeCell current = queue.Dequeue();

            if (current.row != entrance[0] || current.col != entrance[1])
            {
                if (current.row == 0 ||
                    current.row == maze.Length - 1 ||
                    current.col == 0 ||
                    current.col == maze[0].Length - 1)
                {
                    return current.steps;
                }
            }

            int[] rowDelta = { 1, -1, 0, 0 };
            int[] colDelta = { 0, 0, 1, -1 };

            for (int i = 0; i < rowDelta.Length; i++)
            {
                int row = current.row + rowDelta[i];
                int col = current.col + colDelta[i];

                if (row >= 0 &&
                    row < maze.Length &&
                    col >= 0 &&
                    col < maze[0].Length &&
                    maze[row][col] == '.')
                {
                    MazeCell nextCell = new MazeCell(row, col, current.steps + 1);
                    if (!visited.ContainsKey(nextCell.key))
                    {
                        queue.Enqueue(nextCell);
                        visited.Add(nextCell.key, true);
                    }
                }
            }
        }

        return -1;
    }
}